1.はじめに
太陽風と地球磁気圏相互作用の3次元グローバル電磁流体力学的(MHD)シミュレーションは、約20年前に、力が釣り合った平均的な磁気圏の形をやっと再現できるところから出発して、コンピュータとIT技術の長足の進歩に相まって発展を続け、最近では、衛星・地上観測と比較して磁気圏のダイナミックスを議論できる程度にまで成長してきた。こうして、上流の太陽風や惑星間磁場(IMF)の変化に対する磁気圏・電離圏の応答や、磁気圏での大きな擾乱現象であるサブストームや磁気嵐を直接シミュレーションから調べようとする試みも行われるようになってきた。これらの太陽風磁気圏相互作用のグローバルMHDシミュレーションを精度よく実行するためには、計算方法の改良が一方で必要であると同時に、最大級のスーパーコンピュータの利用、それも効率的な並列計算法の利用は不可欠である。
そのような並列計算共通プログラム言語の候補として、High Performance Fortran (HPF)とMessage Passing Interface (MPI)があると言われてきた。HPFは、米国の共同研究者が共通プログラム言語として優れていると言っている反面、多くの大型プログラムで性能が十分に出ないという批判の 声も出ていた。こうした中、2000年からHPF/JA(JAHPFによるHPFの日本拡張版)が使えるようになり、VPP Fortranでフルベクトル化フル並列化されている流体コードやMHDコードは、比較的容易にHPF/JAに書き換えることができて、更にそのHPF/JA のプログラムはVPP Fortranと同等の性能を得ることが示された。しかし、HPF/JAの成功にもかかわらず、HPFの普及は進んでいないのが現状である。こうして、世界標準並列化言語として最後に残ったMPIに対する期待が高まることになる。この講義と実習では、VPP FortranとHPF/JAで書かれた3次元MHDコードとの比較をしながら、MPIを用いた並列計算3次元MHDコードの作成と使用方法を主として解説する。
太陽風磁気圏相互作用などの複雑なシミュレーション結果を理解するためには可視化は必須である。特に、重要でかつ面倒な2つの機能にアニメーション動画作成と3次元可視化があるが、アニメーション動画は時間変化を示すことによって磁気圏ダイナミックスの理解を助け、3次元可視化は磁気圏の流線、磁力線及び電流構造の特徴を明らかにするのに威力を発揮する。さらに、最近話題になっているインターネットによる情報公開は、簡単にはできないような自己矛盾のないシミュレーション結果を誰もが即座に見ることができ、現象をよりよく理解する上で強力な手段となりつつある。
そうした中で、VRML(Virtual Reality Modeling Language)の登場によって、3次元画像処理専用機と3次元画像処理専用ソフトウエアを持たなくても、誰でもVRMLのビューアさえあれば3次元画像を自分の好きなように見ることができる状況が実現した。自分のコンピュータの処理能力に依存するが、ネットスケープやインターネットエクスプローラなどのブラウザを使えば、VRML2.0対応のcosmoplayer等のビューアが標準で付いている。パーソナルコンピュータも最近高速になってきたので、高速のcpuとグラフィックアクセラレータを積み、更に十分なメモリ(256 MB以上)を載せれば、可視化に十分な性能を発揮できる。また、精度の高い3次元画像を快適に見たいのであればWebspaceやCosmoworldsの利用が更に有効である。
2.太陽風磁気圏相互作用の3次元グローバルMHDモデル
太陽風磁気圏相互作用の3次元MHDモデルでは、MHD方程式とマックスウェル方程式を初期値境界値問題として、様々な方法でその時間発展を解いている。偏微分方程式を差分化して2 step Lax-Wendroff法で解く方法などはその例である。空間分解能を上げるための計算方法における様々な工夫として、非一様格子法、非構造格子法、自動調節格子法、時空間多重格子法の導入などが行われている。以下では、私達が3次元MHDシミュレーションに用いている高精度計算法の一つである modified leap-frog 法について述べる[1−4]。
2.1.基礎方程式
MHDモデルの基礎となる規格されたMHD方程式とMaxwell方程式を以下に示す。
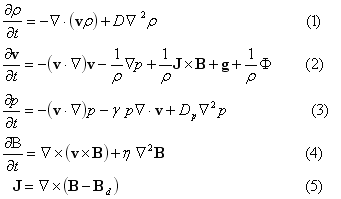
式(1)〜(4)はそれぞれ、連続の式、運動方程式、エネルギー保存則より求まる圧力変化の式、インダクション方程式と呼ばれる磁場変化を示す式である。ただし、ρはプラズマ密度、vは速度ベクトル、pはプラズマ圧力、Βは磁場ベクトルである。この8つのパラメータを未知数として求めていく。ただし、差分法の数値誤差により、Βdに対するJが有限値になるため、式(5)を用いてその数値誤差を除去している。ここでのΒdは地球の固有磁場としての双極子磁場である。また、Φ≡μ∇2 vは粘性項である。η=ηo (Τ/Τo)-3/2 は温度に依存した電気抵抗である。ここでのΤ=p /ρはプラズマ温度であり、Τo は電離層における値で、ηo =0.0005-0.002の範囲にとる。重力項は、g=−go /ζ3(ζ2 =x2 +y2 +z2、 go =1.35×10-7(9.8m/s2))は重力加速度であり、γ=5/3は3次元空間における比熱比である。また、粒子の拡散係数D、圧力の拡散係数Dp、 μの各係数は、初期値や急激な磁場変化に起因する短波長の数値的振動を抑制するために人工的に与えたものであり、D=Dp =μ/ρsw =0.001(ただし、ρsw は太陽風の密度)とした。また、各パラメータは次のものにより規格化した。距離は地球半径Re =6.37×106 m、密度は電離層における値ρs =mns(1010 m-3 )、磁場は赤道における現在の双極子磁場強度Bs =3.12×104 nT、速度は赤道におけるアルフベン速度VA =6.80×106 m/s、時間はアルフベン通過時間ts =Re /VA =0.937sである。
2.2.座標系と境界条件
シミュレーションには、図1に示すような太陽方向x軸正、夕方向y軸正、磁気北極方向z軸正とした太陽地球磁気圏座標系を用いて、MHD方程式とマックスウェル方程式を時空間で差分化して、MHD方程式系における8個の物理変数、プラズマ密度ρ、速度v、圧力p及び 磁場Βの時間発展を解く。ここでは、朝夕と南北で対称性を仮定した1/4領域の地球磁気圏モデルを考える。
Therefore the following boundary conditions are imposed for each physical quantity,
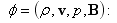
(1)fixed boundary φ= const at x=x0;
(2)free boundary ∂φ/∂x=0 at x=x1;
(3)free boundary at an angle of 45°to the x axis, ∂φ/∂y=0 at y =y0 at ∂φ/∂z =0 at z =z0;
(4) mirror boundary at z =0,
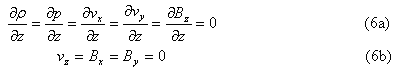
(5) mirror boundary at y =0.

(6) all physical quantities are fixed for
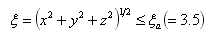
The internal quantity φin at the initial state and the external quantity φex are at each time step connected by the introduction of a smooth function ƒ≡a0h2(a0h2+1) as

where a0=100, h =(ξξa )2-1 for ξ ≥ ξa and h =0 for ξ<ξa.
2.3.初期条件
初期条件には、「対称面より上流で零のミラーダイポール磁場」と「重力とプラズマ圧力が静的に釣り合った球対称の電離層」を仮定し、シミュレーション箱の上流から一定の密度、速度、温度を持つ太陽風を流し始めて、定常状態に近い磁気圏の構造を求める。初期にミラーダイポール磁場を用いる理由は、上流で流れに平行な磁場成分を含めないためである。前述したように、境界条件としては、上流は固定端、側面と上下面は磁気圏前面に形成される衝撃波の形状を考慮して、x軸と45度の角度を持たせた自由端、下流は面に垂直な方向に自由端、地球の中心を通るy=0又はz=0の面では磁場と速度のベクトルと矛盾の無い鏡像の境界条件を課す。更に、太陽風やIMFのパラメータを時間変化させて、磁気圏・電離圏の応答や擾乱現象を調べる。
初期条件の具体的な関数は次の様に与える。
Density
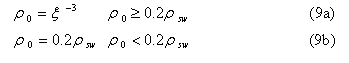
Plasma pressure
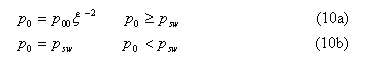
Gravity force

Dipole magnetic field
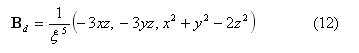
where g0=1.35×10-6 and p00=(γ-1)g0 /γ=5.4×10-7.
The solar wind parameters used are ρsw=5×10-4 (corresponding to 5 cm3 ). vsw =(νsw ,0,0) at x =x 0. νsw=0.0441-0.118(300-800km/s),Psw=3.56×10-8(Tsw=2×105K). and ΒIMF=0 or ±1.5×10-4(±5nT), where ΒIMF stands for the z component of the uniform IMF traveling with the solar wind.
2.4.Modified Leap-Frog法の導入
数値計算法としては、図2に示すようなModified leap-frog法を用いる。最初の1回を two step Lax-Wendroff法で解き、続く (l -1)回を leap-frog法で解き、その一連の手続きを繰り返す。lの値は数値的に安定の範囲で大きい方が望ましいので、2次精度の中心空間差分を採用するとき、数値精度の線形計算と予備的シミュレーションからl = 8に選んでいる。Modified leap-frog法は、two step Lax-Wendroff法の数値的安定化効果を一部取り入れて、leap-frog法の数値的減衰と分散の小さい効果をより多く取り入れた、数値的減衰と分散にバランスの良くとれた一種の組み合わせ計算方法となっている。また、パラメータl を変化させることによって、性質の良く分かった2つの計算方法に一致させることができるので、結果に与える数値誤差の影響も理解し易い利点を持っている。
Modified leap-frog法の具体的な計算スキームを次に示す。先ず次の形の偏微分方程式を導入する。

(1)First step

(2)Second step
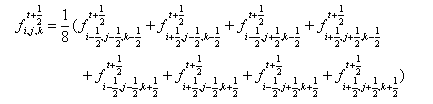 (16)
(16)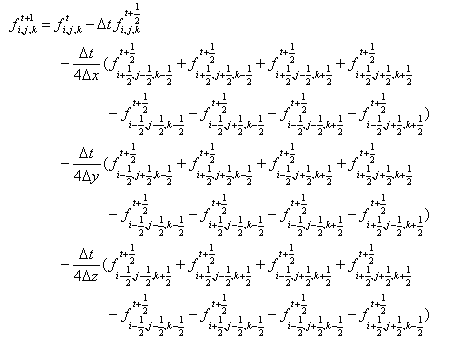 (17)
(17)The concrete procedure of two-step Lax-Wendroff method in the 3-dimensional MHD code is as follows;
1. f (i, j, k) is given for 2 ≤ i ≤ nx1, 2 ≤ j ≤ ny1 and 2 ≤ k ≤ nz 1
2. f (i, j, k) for i =1, nx 2, j =1,ny 2, and k =1, nz 2 is determined from boundary condition
3. 1st interpolation
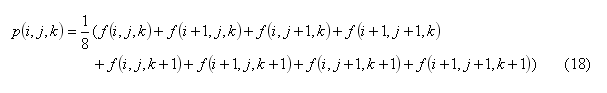

4. Calculation of 1st step
 (20)
(20)5. 2nd interpolation
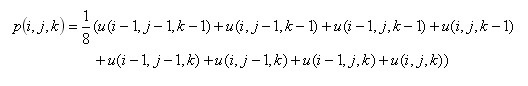 (21)
(21)6. Calculation of 2nd step
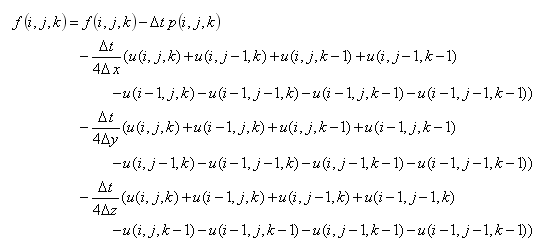 (22)
(22)
この計算スキームは、u (i, j, k)=p (i, j, k) とおく場合two step Lax-Wendroff法となるが、u (i, j, k) に前のステップから計算した値をそのまま使用し、時間幅を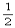 ΔtからΔt と2倍すれば、Leap-frog法になる。Modified leap-frog法は、1回目をtwo-step Lax-Wendroff法、継続する(l -1)回をLeap-frog法を用いて計算する方法である(図2参照)。
ΔtからΔt と2倍すれば、Leap-frog法になる。Modified leap-frog法は、1回目をtwo-step Lax-Wendroff法、継続する(l -1)回をLeap-frog法を用いて計算する方法である(図2参照)。
次に伝達方程式

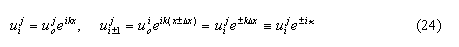
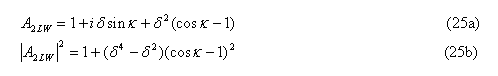
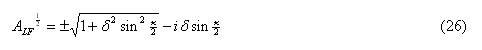

Modified leap-frog法(MLF)、2 step Lax-Wendroff法(2LW)及びRunge-Kutta-Gill法 (RKG)に対する増幅率の絶対値と位相速度の波数依存性を図3に、 l を変化したときのModified leap-frog法(MLF)に対する増幅率の絶対値と位相速度の波数依存性を図4に示す。Modified leap-frog法は絶対値と同様に位相速度に対しても数値精度が大幅に改善されるのが理解される。
Modified leap-frog法、two step Lax-Wendroff法及びleap-frog法の3種類の計算方法を波動方程式に適用した結果を図5に、電磁流体力学の非線形現象であるMHD 衝撃波のシミュレーションに適用した結果を図6に示す。 線形な波動方程式でパルス波の伝搬を差分法で解く場合、波長の短い波ほど数値的減衰が大きくかつ位相速度が遅いので、パルス波が崩れて後に波列が現れる。その数値的な減衰と分散がmodified leap-frog法では大幅に改善されているのが見られる。非線形な現象の場合もtwo step Lax-Wendroff法では、数値的分散によって衝撃波の後ろに振動が発生し、modified leap-frog法では、それが小さく抑えられて衝撃波の形がよく得られているのが分かる。一方、leap-frog法では、振動が深くなって衝撃波がパルス列に分離しているのが見られる。これは、数値的減衰は無いが数値的分散は存在する leap-frog法の数値的特性に依存する現象で物理的には意味のないものである。
3.MPIを用いた並列計算MHDコード
1995年にFujitsu VPP500が使用できるようになって、太陽風と地球磁気圏相互作用のグローバルMHDシミュレーションを実行するためのフルベクトル化されていた3次元MHDコード(earthb)をVPP Fortran用に書き換えた。コードの全面的な書き換えを行って、VPP Fortranで計算効率の高い、ほぼフルベクトル化フル並列化された3次元MHDコード(pearthb)を作成した[荻野、1997]。その後、2000年に3次元MHDコードをVPP FortranからHPF/JAへ書き換えた(hearthb)[荻野、2000; Ogino, 2002]。結果的には、HPF/JAで書いた3次元MHDコード(hearthb)もVPP Fortranの3次元MHDコードと同様にフルベクトル化フル並列化することができ、計算速度もVPP Fortranと同等の性能を得ることができた。VPP Fortranでも、HPF/JAでもベクトル並列化MHDコードとしては、ほとんど同等のものであるが、ベクトル化MHDコード(earthb)とは全く別物である。その最も大きな違いは、ベクトル化MHDコードは、プログラムサイズを最小化しているのに対し、ベクトル並列化MHDコードでは並列計算の性質上プログラムサイズの最小化が不可能だったことである。このため、同じ格子点数のMHDシミュレーションをする場合、ベクトル化コードに比べて、ベクトル並列化コードは約3〜4倍のコンピュータメモリが必要である[荻野、2000; Ogino, 2002]。
2002年になって、周りの人の協力を得てHPF/JAからMPIへとVPP FortranからMPIへの書き換えを行い、MPIでほぼフルベクトル化フル並列化された3次元MHDコード(meartb)を作成することができた。その計算速度は、VPP FortranとHPF/JAのMHDコードと同等以上の高計算効率を得ることができた。書き換えの労力だが、VPP FortranかHPF/JAでフルベクトル化フル並列化された3次元MHDコードがあれば比較的容易にMPI利用のFortranコードに書き換えることが可能である。もちろん、コードによってはフルベクトル化フル並列化を保つために工夫しなければならないことが生じることがある。MPIでの問題点や大規模計算でMPIをどう使用すべきかは、後の補足説明で行う。
ベクトル化や並列化した場合、非ベクトル化コードや非並列化コードに比べて何倍の速度向上率が得られるかを示すものに、アムダールの法則がある。その法則によると、多数のPE(Processing Element)を用いて高い速度向上率を得るためには、並列化率が100%に限りなく近いことが極めて重要となる。従って、高効率のシミュレーションコードを作成するためには、どうやってフルベクトル化とフル並列化を実現するかにかかっている。実際には、内側のdo roopでベクトル化されているので、そのベクトル化を維持したまま外側のdo roopで並列化をすればよいことになる。よく、「計算時間のかかっているdo roopから並列化せよ」と言われるが、その方法だとある程度までは並列化効率が上がるが、100%に近い並列化効率を得ることはほとんど不可能である。これまでのベクトル化と並列化の経験からすると、プログラムの構造をきちんと決めることが最も重要であると確信している。分散メモリ型並列計算機を用いる場合の並列計算の基本は単純なことで、計算する前に計算に必要な変数を全て各PEに集めればよいわけで、それもできるだけ一括して転送し、転送回数をできるだけ少なくすればよい。即ち、プログラムの構造とは、領域分割の変数(方向)を軸とした計算の流れを示すフローチャートに、効率的な配列の利用内容を割り付けたものである。並列計算プログラムでは通常作業配列を多く取る必要が生じるので、プログラムの構造を決める時に作業配列の量を最小にすることが同時に必要となる。
具体的なベクトル並列計算の3次元MHDコードVPP Fortran(pearthb)、HPF/JA(hearthb)、MPI(meartb)を見てもらうと分かるように、その3種類のFortranプログラムの基本的構造はほとんど変わっていない。プログラムの構造をほとんど変えずに、VPP Fortran、HPF/JA、MPIの並列化指示行を挿入することでプログラムの大半の部分を書き換えることができる。それに、それぞれのコンパイラーに特有の部分をユニットとして追加すれば、プログラムの大部分ができあがる。後に残される問題は、大まかに言えば境界条件と入出力である。これらも通常の場合はそれほど深刻な問題とはならない。しかし、MPIで超大型計算まで目標としている場合には、境界条件と入出力には注意が必要である。場合にもよるが、MPIの導入書や解説書に通常書いてある方法はほとんど通用しないと考えておいた方が無難である。
3.1.MPIによるMHDコードの作成(具体例)
MPI(Message Passing Interface)の使い方を分かりやすくかつ具体的に解説したものとして、青山幸也著「並列プログラミング虎の巻 MPI版」がある。その中で、青山氏は、メッセージ交換サブルーチンについて、「並列化にともなう矛盾(副作用)を解消するために、必要最小限仕方なしに行うもの」と言明しているが、全く、達観だと思う。これを私なりに具体的に書くと、「計算する前に、できるだけ一括してかつできるだけ転送回数を少なくして、計算に必要な変数を全て各PE(Processing Element)に集めて計算する」となる。
それでは、MPIによるMHDコードの作成の重要な部分を具体的に見ていくことにする。MPIバージョンのディレクトリmearthbには、二つの基本的なFortranプログラムがある。どちらもこのスクール用のものである。
mearthb_send.f :ブロッキング通信mpi_sendとmpi_recvを利用 mearthb.isend.f :非ブロッキング通信mpi_isendとmpi_irecvを利用した改良版3次元MHDコードは、HPF/JAからMPIへ移植しているので、!hpf$ で示されるHPF/JAの指示行がそのまま残っているが、MPIではそれらは全てコメント行として扱われる。また、MPIへの移植で変更した部分は全て、CC MPI STARTとCC MPI ENDのコメント行で挟まれている。以下では、mearthb_send.fの説明をする。
数値計算法としては、Modified leap-frog法を用いていて、k (z)方向に領域分割を行う。プログラムの計算のパラメータなどは、後の4.1の計算パラメータの設定で詳しく説明しているので、ここでは省略する。PE(Processing Element)数はnpe=2で、isizeはPE数、irankはランク(PE)の番号で、この場合、isize=npe=2、irank=0,1となる。ksとkeはirankでの通常のkの初期値と終期値を示し、各irankのローカルなk=k_localとグローバルなk=k_globalの関係は、k_global=k_local+kssで与えられる。従って、k (z)方向のグローバル変数と並列化後のローカル変数の対応は、
k=1,nz2 -> k=ks,ke k=1,nz2-1 -> k=ks,ke1 k=2,nz2-1 -> k=ks1,ke1となる。また、recvcountとdisplsはgatherする時の各ランクのデータの大きさと各ランクのデータの先頭番地を示す。
CC MPI START
include 'mpif.h'
integer istatus(mpi_status_size)
common /para_info/ks,ks1,ke,ke1,kss,irank,isize
c for mpi_gatherv
parameter (npe=2)
integer recvcount(npe),displs(npe)
CC MPI END
よく使われる1次元方向の分割方法は2種類ある。分割方法1は、あるランクまで同数のkoが入り、それ以後のランクも同数のko-1が入る方法である。分割方法2は、同数のkoが入るランクをできるだけ多く取り、それ以後のランクは順次減らす方法である。ここでは、分割方法1を採用する。この場合あるランクまでに入る同数は、ko=nzz=(nz2-1)/npe+1となる。ここに両側の境界を含めてnz2=nz+2となっている。k (z)方向に分割した両側にのりしろが1個ずつ必要なので、各PEに必要なk (z)方向の配列の範囲はk=(0:nzz+1)で与えられ、大きさはnzz+2と取ればよいことになる。また、fg(nx2,ny2,nz2)はファイルreadとwriteのために利用する作業配列である。
CC MPI START
parameter(nzz=(nz2-1)/npe+1)
dimension f(nx2,ny2,0:nzz+1,nb),u(nx2,ny2,0:nzz+1,nb),
1 ff(nx2,ny2,0:nzz+1,nb),p(nx2,ny2,0:nzz+1,nbb),
2 pp(nx2,ny2,0:nzz+1,3)
c for all_gather
dimension fg(nx2,ny2,nz2)
CC MPI END
分割方法1を用いた、具体的なパラメータは次の部分で与えられる。この計算で、isizeとirankに対する、ks,ke,kss,recvcount(npe),displs(npe)の値が決められる。recvcount(npe)を計算するのに、mpi_gatherを用いている。この部分はそのまま他のプログラムにも利用できて、それが、理解できるとMPIの1次元方向の分割方法は主な部分が分かったことになる。
CC MPI START
call mpi_init(ier)
call mpi_comm_rank(mpi_comm_world,irank,ier)
call mpi_comm_size(mpi_comm_world,isize,ier)
c
kk=nz2/isize
kmod=mod(nz2,isize)
c
ks=1
kss=irank*kk+min(kmod,irank)
c
if (irank.lt.kmod) kk=kk+1
ke=ks+kk-1
ks1=ks
ke1=ke
if (irank.eq.0) ks1=2
if (irank.eq.isize-1) ke1=ke-1
c
nword=(ke-ks+1)*nx2*ny2
call mpi_gather(nword,1,mpi_integer,recvcount,
* 1,mpi_integer,0,mpi_comm_world,ier)
displs(1)=0
do i=2,isize
displs(i)=displs(i-1)+recvcount(i-1)
end do
c
CC MPI END
次の2つは、単純なことでデータのread、write及びファイルの入出力はirank=0で実行することを宣言している。
CC MPI START
if (irank.eq.0) then
open(11,file='./school/mearthb/meart01.data',
1 access='sequential',form='unformatted')
end if
CC MPI END
CC MPI START
if (irank.eq.0)
* write (6,12) iii,last,nx,ny,nz,n1,n2,n3,n4,n5,n6,eat0,rmu0,aru,
1 eud,rrat,hx,hy,hz,t,t1,ro01,pr01,gra,dx2,dy2,dz2,dx4,dy4,dz4,
2 bis,(cp(i),i=1,11),(cj(j),j=1,10)
CC MPI END
また、k (z)方向には領域分割されているので、k (z)方向のグローバルな変数k=1,nz2は必ずロー
カルな変数k=ks,keに変更しなければならない。
CC MPI START
do 22 k=ks,ke
CC MPI END
次の部分は、ブロッキング通信を用いて、irankのksのデータをirank-1にmpi_sendで送り、そのデータをirank+1からirankのke+1に転送することで、のりしろのデータを一つ若いランクのPEに送る。mpi_barrierは同期を取るためである。
CC MPI START
do m=1,nb
len=nx2*ny2
if (irank.gt.0) then
call mpi_send(f(1,1,ks,m),n2,mpi_real,irank-1,
& 100,mpi_comm_world,ier)
end if
if (irank.lt.isize-1) then
call mpi_recv(f(1,1,ke+1,m),n2,mpi_real,irank+1,
& 100,mpi_comm_world,istatus,ier)
end if
end do
call mpi_barrier(mpi_comm_world,ier)
CC MPI END
次は、mpi_gathervでデータをirank=0に全て集めて、irank=0でファイルに書き出している。この
時、書き出しの前にmpi_barrierで同期を取る必要がある。
do 173 m=1,nb
CC MPI START
c do m=1,nb
call mpi_barrier(mpi_comm_world,ier)
call mpi_gatherv(f(1,1,1,m),nword,mpi_real,fg(1,1,1),
* recvcount,displs,mpi_real,0,
* mpi_comm_world,ier)
c end do
call mpi_barrier(mpi_comm_world,ier)
CC MPI END
CC MPI START
if(irank.eq.0) then
CC MPI END
do 1732 k=1,nz2
write(ntap) fg(1:nx2,1:ny2,k)
1732 continue
CC MPI START
end if
CC MPI END
173 continue
また、MHDシミュレーションを続ける時、常に速度の絶対値の最大値をモニターすることによって、数値不安定が生じたかどうかを判定していて、vmaxが規格化した値で1を越えたら、その時のデータを書き出して計算を終了するようにしている。そのvmaxの計算には、mpi_allreduceを用いる。
CC MPI START
call mpi_allreduce(vmax,vmax1,1,mpi_real,mpi_max,
* mpi_comm_world,ier)
vmax=vmax1
CC MPI END
以上みてきたように、HPF/JAのプログラムをMPIに書き換える場合、CC MPI STARTとCC MPI ENDで挟まれるテンプレート(モジュール)を追加・置き換えすれば、ほとんどそのまま書き換えることができる。VPP FortranからMPIへの書き換えもほとんど同じである。こうして、MPIに書き換えられた3次元MHDコードは、ほとんどベクトル化と並列化がされていると考えてよい。もちろん、時々、境界条件の部分で新たな工夫が必要なことが生じることがある。また、中規模までの計算では効率的な計算が行えたとしても、超大規模計算(3次元MHDで約1億以上の格子点を使用)の場合は、更なる注意と考慮が必要である。
3.2.MPI利用についての補足説明
MPI利用で、並列計算効率の高いプログラムの作成、境界条件の扱い方、ファイルのreadとwriteについて、補足説明を行う。
(1) 非ブロッキング通信の使用
前の節では、ブロッキング通信mpi_sendとmpi_recvを利用していたが、非ブロッキング通信mpi_isendとmpi_irecvを使用するとプログラムの計算効率が向上する。その使用方法は簡単で、使用例はmearthb.isend.fにあるのでご覧頂きたい。この場合、非ブロッキング通信を用いるので、送信mpi_isendと受信mpi_irecvコマンドと同時に送信・受信の完了を待つmpi_waitをセットにして用いる必要がある。
(2) 周期的境界条件
周期的境界条件は、次のように最後の番号のPE、irank=isize-1のk=ke-1から、最初の番号のPE、irank=0のk=ksへと転送し、更に、最初の番号のPE、irank=0のk=ks+1から最後の番号のPE、irank=isize-1のk=keへと転送すればよい。その具体的な例は、次に示すようなModified leap-frog法で3次元の波動方程式を解くプログラム、ディレクトリmwaveのmwave3.f.sendとmwave3.f.isendを参照して頂きたい。
CC MPI START
if (irank.eq.isize-1) then
call mpi_send(f(1,1,ke-1,m),n2,mpi_real,0,
& 110,mpi_comm_world,ier)
elseif (irank.eq.0) then
call mpi_recv(f(1,1,ks,m),n2,mpi_real,isize-1,
& 110,mpi_comm_world,istatus,ier)
end if
c
if (irank.eq.0) then
call mpi_send(f(1,1,ks+1,m),n2,mpi_real,isize-1,
& 115,mpi_comm_world,ier)
elseif (irank.eq.isize-1) then
call mpi_recv(f(1,1,ke,m),n2,mpi_real,0,
& 115,mpi_comm_world,istatus,ier)
end if
call mpi_barrier(mpi_comm_world,ier)
CC MPI END
(3) 特殊な境界条件をMPIでどう解くか
次の例のように、分割のk(z)方向の変数を逆に並び替える場合は、効率のよいMPIのプログラムをどのように作るか、考えてみて下さい。ここに、nz2=nz+2,nz3=nz+3とする。(ヒント:必要最小の変数をmpi_gathervでirank=0に集めて、並び替え、続いてmpi_scattervで各PEに配信する方法が考えられる。)
do k=1,nz2
f(2:nx1,1,k,1:nb) = f(2:nx1,2,-k+nz3,1:nb)
end do
(4) readとwriteのファイル入出力をどうするか
地球磁気圏の3次元MHDコードmearthb_send.fでは、データ入出力の作業配列fg(nx2,ny2,nz2)を用意して、mpi_gathervでデータをirank=0に全て集めて、irank=0でファイルに書き出している。これは、配列を増やしてプログラムサイズを大きくする時、大きな問題となる。まず、送受信のバッファーの制限内に収まっているか、次にirank=0のfg(nx2,ny2,nz2)にデータを全て集めるので、irank=0のメモリ制限がある。通常の計算(3次元MHDコードでの格子点が約1億個以下)では、ここで書いていることは深刻な問題とはならない。しかし、プログラムサイズを極端に大きくする時は作業配列fgは使用せず、かつデータをirank=0に全て集めることも止める必要がある。この場合は、個々のランク(PE)からそれぞれ名前を区別して個々にファイルを書き出し、後でその個々のファイルをまとめるなど編集して利用することになる。
(5) MPIのプログラム作成のまとめ
これまでみてきたように、MPIのプログラム作成は簡単だと思って間違いはないと思う。それも、VPP FortranやHPF/JAで効率的に書かれたプログラムならなおさらである。そして、フルベクトル化とフル並列化も多くの場合、容易に達せられるであろう。問題が生じるとすれば、境界条件で発生することが時々ある。また、MPIプログラムの高効率化は使用している並列計算機の特徴や機能とも関係している。従って、問題が生じたり、高効率化が出ない場合は、センターなどのプログラム相談者に質問や相談するのがよいであろう。それと並行して、MPIプログラムを利用している研究者がMPIの使用知識を公開して共有化することも極めて現実的で有効な方法である。この目的で私達は次のHomepage(http://center.stelab.nagoya-u.ac.jp/kaken/kakenhi.html)を設けて、個々の研究者が得た並列計算の知識を共有化しようと計画している。
3.3.並列計算法の効率
3次元MHDシミュレーションなどの大型シミュレーションを実行するためには、スーパーコンピュータの利用と、ベクトル化や並列化による計算速度の効率化は必須である。表1に、講義と実習で使用する3次元MHDコードをSUNとVPP-5000(VP Fortran, VPP Fortran, HPF/JA, MPI)で実行した時の速度の比較を示している。計算時間(sec)は、Modified leap-frog法で1回時間ステップを進めるのに要する時間を示している。SUN(GR720)に比べて、VPP5000(2PE)ではいずれも約70倍の計算速度がでていることが分かる。実際の太陽風地球磁気圏相互作用の3次元MHDシミュレーションでは、約1万回の繰り返し計算をするので、SUN(GR720)で約20時間、VPP5000(2PE,MPI)で約20分の計算時間がかかることが分かる。PEを増やすと更にその差は更に大きくなる。
表1.計算機実習で用いる1/4領域の地球磁気圏シミュレーション3次元MHDコードの
計算速度の比較:earthb、格子点数(nx,ny,nz)=(180,60,60)
Table 1. Comparison of computer processing capability of 3-dimensional global
MHD code with a quarter volume: earthb with (nx,ny,nz)=(180,60,60).
-----------------------------------------------------------------------------------------------------------------------
Computer Processing Capability
A Quarter Model of the Earth's Magnetosphere (nx,ny,nz)=(180,60,60); earthb
computer number of PEs compiler sec (MFLOPS) GF/PE (date)
----------------------------------------------------------------------------------------------------------------------
Fujitsu GR720 (1PE) Fortran 90 (frt) 7.72998 ( 136) 0.14 (2002.08.01)
Fujitsu VPP-5000 (1PE) VP Fortran 0.19342 ( 5,428) 5.43 (2002.08.01)
Fujitsu VPP-5000 (2PE) VPP Fortran 0.10509 ( 9,990) 5.00 (2002.08.01)
Fujitsu VPP-5000 (2PE) HPF/JA 0.11064 ( 9,489) 4.74 (2002.08.01)
Fujitsu VPP-5000 (2PE) MPI 0.09899 ( 10,606) 5.30 (2002.08.01)
Fujitsu VPP-5000 (2PE) MPI (isend) 0.09774 ( 10,797) 5.40 (2002.08.08)
------------------------------------------------------------------------------------------------------------------------
frt: Fujitsu VPP Fortran 90 HPF: High Performance Fortran
MPI; Massage Passing Interface
: MFLOPS is an estimated value in comparison with the computation by
1 processor of CRAY Y-MP C90.
並列計算法の有効性を示すために、VPP FortranとHPF/JAとMPIで書かれた太陽風地球磁気圏相互作用の3次元MHD コードによるFujitsu VPP5000/64を用いての計算速度の比較を示す。VPP Fortran, HPF/JA及びMPIで同等の計算速度がでていて、その計算効率もかなり高いことが分かる。これらの並列計算MHDコードはフルベクトル化とフル並列化ができていて、VPP FortranとHPF/JAの大規模計算では400 Gflops程度以上の高効率も実現している。こうして、ワークステーションやPCの最速のものに対して、最大規模のスーパーコンピュータは大体千倍以上の計算速度を有していることが理解できると思う。
配列が(800x200x478, 800x200x670)のように大きくなって、計算の規模が大きくなった場合、MPIは通常のオペレーションモードではまだ必ずしも十分な高効率の計算速度を実現していない。表2では、MPI Fortranジョブも高効率が得られているが、これはシングルモードでのテスト結果を示している。通常のオペレーションモードで必ずしも高効率が得られない理由は、当該のMPI Fortran コードの問題、ベクトル並列型スーパーコンピュータVPP5000とのマッチングの問題、MPIの計算時間計測のみが他と異なっている問題などいくつかの原因があるようなので、目下調査中である。問題がはっきりすれば、上述のHomepageなどで示す予定である。VPP FortranとHPF/JAではcpu使用時間の累計を計算時間計測に用いているが、MPIではcpu使用時間の累計を計る方法が無いので単にジョブの経過時間を用いている。従って、MPIの計測では多重のジョブが同時に実行されているとそれだけ遅く出てしまう。いずれにせよ、MPIは使用開始して日が浅いので、解決すべき問題が多くある。MPIは最後の共通並列計算方法である点からも、その問題解決のためにもMPIの使用知識の共有化は重要であると考えている。
表2.VPP FortranとHPF/JAとMPIで書かれた太陽風地球磁気圏相互作用の3次元MHD コードによる Fujitsu VPP5000/64での計算速度の比較
Table 2. Comparison of computer processing capability between VPP Fortran and HPF/JA and MPI
in a 3-dimensional global MHD code of the solar wind-magnetosphere interaction by using Fujitsu VPP5000/64.
-------------------------------------------------------------------------------------------------------------------------------------
Number Number of VPP Fortran HPF/JA MPI
of PE grids cpu time Gflops Gf/PE cpu time Gflops Gf/PE cpu time Gflops Gf/PE
-------------------------------------------------------------------------------------------------------------------------------------
1PE 200x100x478 119.607 ( 0.17) 0.17 (scalar)
1PE 200x100x478 2.967 ( 6.88) 6.88 3.002 ( 6.80) 6.80
2PE 200x100x478 1.458 ( 14.01) 7.00 1.535 ( 13.30) 6.65 1.444 ( 14.14) 7.07
4PE 200x100x478 0.721 ( 28.32) 7.08 0.761 ( 26.85) 6.71 0.714 ( 28.60) 7.15
8PE 200x100x478 0.365 ( 55.89) 6.99 0.386 ( 52.92) 6.62 0.361 ( 56.55) 7.07
16PE 200x100x478 0.205 ( 99.38) 6.21 0.219 ( 93.39) 5.84 0.191 (107.19) 6.70
24PE 200x100x478 0.141 (144.49) 6.02 0.143 (143.02) 5.96 0.1302(157.24) 6.55
32PE 200x100x478 0.107 (191.23) 5.98 0.110 (186.13) 5.82 0.1011(202.50) 6.33
48PE 200x100x478 0.069 (297.96) 6.21 0.074 (276.96) 5.77 0.0679(301.51) 6.28
56PE 200x100x478 0.064 (319.53) 5.71 0.068 (299.27) 5.34 0.0639(320.39) 5.72
64PE 200x100x478 0.0662(308.91) 4.83 0.0627(324.57) 5.07 0.0569(359.80) 5.62
1PE 500x100x200 2.691 ( 7.94) 7.94 2.691 ( 7.94) 7.94
2PE 500x100x200 1.381 ( 15.47) 7.73 1.390 ( 15.37) 7.68 1.355 ( 15.77) 7.89
4PE 500x100x200 0.715 ( 29.97) 7.47 0.712 ( 29.99) 7.50 0.688 ( 31.03) 7.76
8PE 500x100x200 0.398 ( 53.65) 6.71 0.393 ( 54.38) 6.80 0.372 ( 57.50) 7.19
16PE 500x100x200 0.210 (101.87) 6.37 0.202 (105.74) 6.61 0.193 (110.70) 6.92
24PE 500x100x200 0.160 (133.70) 5.57 0.150 (142.40) 5.93 0.135 (158.26) 6.59
32PE 500x100x200 0.131 (163.55) 5.11 0.120 (175.50) 5.48 0.1084(197.10) 6.15
48PE 500x100x200 0.100 (214.48) 4.46 0.091 (231.69) 4.82 0.0811(263.44) 5.49
56PE 500x100x200 0.089 (239.48) 4.28 0.086 (244.85) 4.37 0.0688(310.54) 5.55
64PE 500x100x200 0.0956(222.95) 3.48 0.0844(249.49) 3.90 0.0687(310.99) 4.86
2PE 800x200x478 10.659 ( 15.33) 7.66 10.742 ( 15.21) 7.60 10.428 ( 15.67) 7.83
4PE 800x200x478 5.351 ( 30.53) 7.63 5.354 ( 30.52) 7.63 5.223 ( 31.28) 7.82
8PE 800x200x478 2.738 ( 59.67) 7.46 2.730 ( 59.85) 7.48 2.696 ( 60.61) 7.58
12PE 800x200x478 1.865 ( 87.58) 7.30 1.911 ( 85.49) 7.12 1.771 ( 92.25) 7.68
16PE 800x200x478 1.419 (115.12) 7.19 1.389 (117.66) 7.35 1.342 (121.81) 7.61
24PE 800x200x478 0.975 (167.54) 6.98 0.976 (167.45) 6.98 0.905 (180.59) 7.52
32PE 800x200x478 0.722 (226.33) 7.07 0.717 (227.72) 7.12 0.690 (236.63) 7.39
48PE 800x200x478 0.534 (305.70) 6.36 0.515 (317.26) 6.61 0.469 (348.38) 7.25
56PE 800x200x478 0.494 (330.95) 5.91 0.464 (352.49) 6.29 0.433 (377.73) 7.74
64PE 800x200x478 0.465 (351.59) 5.49 0.438 (373.41) 5.83 0.389 (420.45) 6.57
4PE 800x200x670 7.618 ( 30.06) 7.52 8.001 ( 28.62) 7.16 7.433 ( 30.81) 7.70
8PE 800x200x670 3.794 ( 60.36) 7.54 3.962 ( 57.81) 7.23 3.683 ( 62.17) 7.77
12PE 800x200x670 2.806 ( 81.61) 6.80 3.005 ( 76.21) 6.35 2.696 ( 84.95) 7.08
16PE 800x200x670 1.924 (119.00) 7.44 2.012 (113.85) 7.12 1.854 (123.53) 7.72
24PE 800x200x670 1.308 (175.10) 7.30 1.360 (168.44) 7.02 1.254 (182.61) 7.60
32PE 800x200x670 0.979 (233.85) 7.31 1.032 (221.88) 6.93 0.955 (239.77) 7.49
48PE 800x200x670 0.682 (335.62) 6.99 0.721 (317.80) 6.62 0.662 (346.21) 7.21
56PE 800x200x670 0.595 (384.61) 6.87 0.628 (364.87) 6.52 0.572 (400.59) 7.15
16PE 1000x500x1118 9.668 (123.52) 7.72 9.619 (125.50) 7.84
32PE 1000x500x1118 5.044 (236.73) 7.40 4.992 (241.83) 7.56
48PE 1000x500x1118 3.550 (336.40) 7.01 3.479 (346.97) 7.23
56PE 1000x500x1118 2.985 (400.04) 7.14 2.935 (411.36) 7.35
32PE 1000x1000x1118 9.979 (239.33) 7.48 9.813 (243.37) 7.61
48PE 1000x1000x1118 7.177 (332.79) 6.93 7.028 (339.85) 7.08
56PE 1000x1000x1118 5.817 (410.55) 7.33 5.794 (412.23) 7.36
-------------------------------------------------------------------------------------------------------------------------------------
: Mflops is an estimated value in comparison with the computation by
1 processor of CRAY Y-MP C90.
4.太陽風磁気圏相互作用の3次元MHDコードの実行
ここでは、計算機実習で用いる1/4領域の太陽風と地球磁気圏相互作用の3次元グローバルMHDシミュレーションコードで用いているパラメータの説明をして、ワークステーションなどの普通の計算機で計算するメモリ節約型のベクトル化コード(earthb10.f)、及び、VPP Fortran, HPF/JA及びMPIの3つのバージョンの並列計算3次元MHDコードの計算実行方法とその具体例を示す。
3-Dimensional MHD Simulation of Earth's Magnetosphere
<< Example to execute the MHD Code and Graphic programs >>
We will demonstrate how to execute the 3-Dimensional magnetohydrodynamic (MHD) Simulation of Earth's Magnetosphere in 1/4 volume and how to use the graphics programs to make PostScript files and VRML files in this section. In the MHD model, MHD and Maxwell's equations are solved in the solar-magnetospheric coordinate system by using modified leap-frog method when the upstream solar wind and interplanetary magnetic field (IMF) boundary conditions are given. Moreover, north-south symmetry and dawn-dusk symmetry are assumed, therefore it is enough to solve 1/4 volume as the simulation box. The main simulation Fortran program, earthb10.f is fully vectorized and can be executed on many kinds of computers. By executing the main MHD simulation code, a simulated binary file is produced as output. When the output binary file is used as input, graphics programs can be executed to make PostScript files and VRML files for three dimensional visualization.
4.1.計算パラメータの設定
ベクトル化された3次元MHDコードearthb(earthb10.f)で使用しているパラメータの設定を次にまとめて示す。ベクトル並列化3次元MHDコードでのパラメータの設定内容は同じである。
main program : earthb10.f
earthb10.f using modified leap-frog scheme
3D MHD simulation of 1/4 earth's magnetosphere
Cartesian coordinate finite resistivity 45 degree boundary
(nx,ny,nz)=(180,60,60) : grid number without boundary
nxp=30 : parameter to determine earth position
last=1024 : number of time steps
iiq0=8 : a unit of modified leap-frog scheme
iip0= 32 : adjust upstream boundary condition
iis0= 1024 : sampling step of data
thx=4.00 : parameter to adjust time step
(xl,yl,zl)=(90.5,30.5,30.5)Re: length in each direction
hx=xl/float(nx+1)=0.5Re : grid interval in x direction
hy=yl/float(ny+1)=0.5Re : grid interval in y direction
hz=zl/float(nz+1)=0.5Re : grid interval in z direction
t=0.5*hx*thx : time interval
t(real)=t*ts : real time to one time step advance
=0.5*0.5*4.00*0.937 : ts is normalization value in time
=0.937 sec
x=0.5*hx*float(2*i-nx2-1+2*nxp) : x position versus grid number
y=0.5*hy*float(2*j-3) : y position versus grid number
z=0.5*hz*float(2*k-3) : z position versus grid number
where nx2=nx+2, ny2=ny+2 and nz2=nz+2
ro01=5.0E-4 (5/cc) : mass density of solar wind
pr01=3.56E-8 : pressure of solar wind
vsw=0.044 (300km/s) : speed of solar wind
bis=CP(11)=1.5E-4 (5nT) : amplitude of IMF
eatt : resistivity
rmuu : viscosity
eud0 : friction or collision term
1-dimensional array variable f(i1)=f(i,j,k,m)
n1=nx+2,n2=n1*(ny+2),n3=n2*(nz+2)
nb=8,nbb=11,n4=n3*nb,n5=n3*nbb
i1=i+n1*(j-1)+n2*(k-1)+n3*(m-1)
m=1 : rho, plasma density
m=2 : Vx, x-component of velocity
m=3 : Vy, y-component of velocity
m=4 : Vz, z-component of velocity
m=5 : P, plasma pressure
m=6 : Bx, x-component of magnetic field
m=7 : By, y-component of magnetic field
m=8 : Bz, z-component of magnetic field
4.2.計算実行例
ベクトル化された3次元MHDコードearthb(earthb10.f)とベクトル並列化3次元MHDコード、MPI(mearthb)、HPF/JA(hearthb)、VPP Fortran(peartb)での計算実行例を次に示す。ベクトル並列化3次元MHDコードの実行でコンパイルと実行のシェルは、それぞれのディレクトリの中に置いてあり、実行コマンドの例はreadmeファイルに書かれている。
4.2.1. << execution of main program >>
1. f77 -O earthb10.f
2. a.out &
where file must be defined in open statement like
c open(10,file='earthb10.data',
c 1 access='sequential',form='unformatted')
open(11,file='earthb11.data',
1 access='sequential',form='unformatted')
c
or
1. f77 -o earthb10 -O earthb10.f
2. earthb10 &
4.2.2. << compile and execution using by supercomputer, Fujitsu VPP5000 >>
(1) MPI (Massage Passing Interface): mearthb
All the comand shells are in "readme" file.
(1a) TSS
mpifrt progmpi.f :compile to make execution file, a.out
jobexec -vp 2 ~/school/mearthb/a.out :execution of a.out by 2 PEs
(1b) Batch
qsub -q c -eo -o pconpmpi2.out pcompmpi2.sh :compile
qsub mpi_lim02e.sh :execution of progmpi by 2 PEs
(2) HPF/JA (High Performance Fortran): hearthb
qsub -q c -eo -o pconphpf2.out pcomphpf2.sh :compile
qsub -q z -eo -lPv 2 -o pexechpf.out pexechpf.sh :execution by 2 PEs
qsub -q c -eo -o comp.out comp.sh :compile vector mode only
qsub -q x -eo -o exec.out exec.sh :execution by 1 PE
(3) VPP Fortran (Fortran 90): pearthb
qsub -q c -eo -o pcomp90.out pcomp90.sh :compile
qsub -q z -eo -lPv 2 -o pexec90.out pexec90.sh :execution by 2 PEs
4.3.図形処理
図形処理を統一的に行うためには、次の3つの条件が満たされる必要がある。 1.コンピュータの種類に依存しない方法の確立 2.ソフトウエアなど全てを自分たちでコントロールする 3.プログラムなどできるだけ統一的に(共通に)扱う方法の確立これを逆にいえば、コンピュータに依存したソフトウエアや言語・仕様は使わない、また、特定の業者のみが販売する図形処理応用ソフトウエアは使わない、ということになる。紆余曲折したが、画像処理と図形出力の統一的な扱いのためには、Fortranなどを用いてPostScript画像ファイルを直接作成することが有効な方法であるという結論に達した。その結果として、私達が現在行っているコンピュータシミュレーションの画像処理の統一的な方法を項目としてまとめると以下のようになる。
(1) シミュレーションデータをIEEE Binary形式で保存 (2) FortranプログラムでPostScript画像ファイルを直接に作成 PostScriptファイルを作成するためのInterface Subroutine Packageを作成 (3) PostScriptファイルからファイル変換ツール(xv, pstogifなど)で圧縮された 画像ファイル(gifなど)を作成 (4) 圧縮画像ファイル(gifなど)をWWWで公開
この方法により、Fortranが使えて、その中で大文字と小文字の区別ができれば、コンピュータの種類によらずにPostScript画像ファイルを作って図形出力を取り出すことが可能になった。また、C言語でもできるようにC言語用のInterface Subroutine Packageも用意している。
http://gedas.stelab.nagoya-u.ac.jp/simulation/jst2k/hpf02.html
4.3.1. graphics program to make PostScript files
1. gm150b.f (main) + gsub150.f (subroutine)
noon-midnight meridian and equatorial plots (black and white)
2. gm220b.f (main) + gsub220.f (subroutine)
energy distribution of cross section
3. gm480b.f (main) + gsub480.f (subroutine)
3-dimensional magnetic field lines
<< execution of PostScript graphics program >>
1. f77 -c -O gsub150.f
2. f77 -O gm150b.f gsub150.o
3. a.out > gm150b.ps &
4. gs gm150b.ps
5. lp gm150b.ps
1. f77 -c -O gsub220.f
2. f77 -O gm220b.f gsub220.o
3. a.out > gm220b.ps &
1. f77 -c -O gsub480b.f
2. f77 -O gm480b.f gsub480b.o
3. a.out & : output is written in fort.10
4. mv fort-10 gm480b.ps
太陽風と地球磁気圏相互作用の3次元グローバルMHDシミュレーションから得られた地球磁気圏の構造を示す図を、図7.子午面と赤道面及び尾部断面図(白黒:gm150b.ps)、図8.子午面と赤道面及び尾部断面図(カラー図:gm220b.ps)、図9.磁力線の3次元構造(gm480b.ps)に示す。
5.VRMLによる3次元可視化
VRML(Virtual Reality Modeling Language)の登場のよって、VRMLのビューアさえあれば誰でも3次元画像を自分の好きなように見ることができる状況が実現した。自分のコンピュータの処理能力に依存して3次元画像処理(回転、拡大縮小など)の速度は決まるが、最近のネットスケープやインターネットエクスプローラなどを使えば、VRML2.0対応のcosmo player等のビューアを利用して、3次元可視化がいつでもどこでも実現できる。
VRMLファイルの作成をどう実現するかであるが、私達は、VRMLファイル作成のための Fortran Interface Subroutine Packageを準備し、フォートランプログラムを用いて、3次元シミュレーションデータから直接にVRMLファイル(*.wrl)を作っている。これは3次元と2次元の違いはあるが、PostScript画像ファイルを作成する方法と同様の方法である。VRMLのビューアには通常視点を移動するwalkモードと対象物を移動・回転・拡大縮小するexamineモードがあり、磁気リコネクションなどの微細構造の関係を見るのに大変有効である。
5.1.Fortranを用いたサブルーチンパッケージ
ftp://gedas.stelab.nagoya-u.ac.jp/sramp/simulation/vrml/
VRML (Virtual Reality Modeling Language) and PostScript Fortran programs
1. vrml
3-dimensional visualization Fortran program by using VRML
2. PostScript
Fortran test program to make PostScript graphic files
3. PostScript2
Fortran test program to make PostScript graphic files with subroutine
5.2.地球磁気圏の3次元MHDシミュレーションへの適用
ftp://gedas.stelab.nagoya-u.ac.jp/sramp/simulation/earthb/
3-dimensional graphics program by VRML files
< Virtual Reality Modeling Language >
1. zvrmagb.f (main) + zvrsubb.f (subroutine)
3-dimensional magnetic field lines
2. zvrcrob.f (main) + zvrsubb.f (subroutine)
cross sectional pattern by pixel image
<< execution of VRML graphics program >>
1. f77 -c -O zvrsubb.f
2. f77 -O zvrmagb.f zvrsubb.o
3. a.out & : output is written in fort.10
4. mv fort.10 fort.102
1. f77 -c -O zvrsubb.f
5. f77 -O zvrcrob.f zvrsubb.o
6. a.out & : output is written in fort.10
7. mv fort.10 fort.101
8. cat fort.101 fort.102 > zvrml01.wrl
VRMLを用いて、シミュレーションから得られた地球磁気圏構造を3次元可視化した例を図10に示す。
6.おわりに
富士通VP-2600、日立S820、NEC SX-3、CRAY Y-MPなどのベクトル計算機の時代までは、フルベクトル化された3次元MHDコードを用いてFortranコンパイラーが載っている全ての計算機を利用して、太陽風と地球磁気圏相互作用の3次元グローバルMHDシミュレーションを実行することができた。このFortranプログラムの汎用性のために、私達は3次元MHDコードを世界中どこででも動かすことができ、MHDコードの配布などを通して世界中の多くの研究者と共同研究を行うことができた。しかし、ベクトル並列機と超並列機がコンピュータ シミュレーションの世の中に現れてくるや否や、Fortranプログラムの並列化の効率を上げるためにコンピュータに依存した様々の異なった手法を採らなければならなくなった。多くのシミュレーション研究者は共通のプログラム言語を失い、特定のメーカーの機種でしか並列化の効率を上げられない、方言のFortranプログラム言語を使わざるを得ない状況が発生した。
そのような閉塞的な状況を打開する並列計算共通プログラム言語の候補として、HPF (High Performance Fortran) とMPI (Message Passing Interface)がある。HPFで書かれたコードは、日米のほとんどのスーパーコンピュータで高効率の計算が期待できないし、その改良版のHPF/JA(日本で開発改良されたHPFの改良版)は高効率が実現できるが、それも現在は日本の富士通とNECのスーパーコンピュータに限定され、日立のマシンでは高効率を得ることはできない。こうして、共通並列計算法としてのMPIに対する期待は益々大きくなっていた。こうした状況下、MPIを用いた3次元MHDコード作成の具体的方法を例示し、VPP FortranやHPF/JAと同等以上の高効率計算が実現できることを具体的に示してきた。MPIは、今後画像処理なども含めて、多くの種類の計算機で広く並列計算に使われる方法として期待されている。
太陽風と地球磁気圏相互作用のシミュレーション結果などを理解し、更に、人によりよく理解してもらうためには可視化は必須であり、アニメーション動画の作成と3次元可視化/3次元画像解析は極めて強力な威力を発揮する。動画によってその複雑な振る舞いを一目瞭然にすることができ、更に、インターネット3次元言語、VRMLの登場によって3次元画像解析を誰にでもすぐに手にすることができるようになった。即ち、ネットワークを通して3次元可視化コンテンツの共有化が実現できるようになったといえる。
世界最高速の性能を誇る国産の新世代並列型スーパーコンピュータを用い、スペースプラズマ現象を効率よく並列計算できる、HPFやMPIの共通コンピュータ言語を用いた電磁流体コード、粒子コード、及びハイブリッドコードを作成・普及させて、世界に先駆けた大規模シミュレーションとそれらのコードを連携した大規模シミュレーションから太陽風磁気圏電離圏ダイナミックスやスペースプラズマの非線形物理に新しい知見をもたらすことが期待される。
謝辞
本稿のコンピュータシミュレーションは名古屋大学情報連携基盤センターのスーパーコンピュータ、Fujitsu VPP5000/64を利用してなされたものです。また、VPP FortranからHPF/JAとMPIへの書き換えでは多くの助言を頂いた名古屋大学情報連携基盤センターの津田知子助手と富士通株式会社の方に、更に、MPIへの原型の書き換えではお世話と指導頂いた国立極地研究所の岡田雅樹助手と日立製作所の方に感謝いたします。
[参考文献]
[1] T. Ogino, A three-dimensional MHD simulation of the interaction of the solar wind with the
earth's magnetosphere: The generation of field-aligned currents,
J. Geophys. Res., 91, 6791-6806 (1986).
[2] T. Ogino, R.J. Walker and M. Ashour-Abdalla, A global magnetohydrodynamic simulation of the
magnetosheath and magnetopause when the interplanetary magnetic field is northward,
IEEE Transactions on Plasma Science, Vol.20, No.6, 817-828 (1992).
[3] T. Ogino, Two-Dimensional MHD Code, (in Computer Space Plasma Physics), Ed. by H.
Matsumoto and Y. Omura, Terra Scientific Publishing Company,
161-215, 411-467 (1993).
[4] T. Ogino, R.J. Walker and M. Ashour-Abdalla, A global magnetohydrodynamic simulation of the
response of the magnetosphere to a northward turning of the interplanetary magnetic field,
J. Geophys. Res., Vol.99, No.A6, 11,027-11,042 (1994).
[5] 荻野竜樹、「太陽風と磁気圏相互作用の電磁流体力学的シミュレーション」,
プラズマ・核融合学会誌,CD-ROM 特別企画(解説論文), Vol.75, No.5, CD-ROM 20-30, 1999.
http://gedas.stelab.nagoya-u.ac.jp/simulation/mhd3d01/mhd3d.html
[6] 荻野竜樹、「太陽風磁気圏相互作用の計算機シミュレーション」,
名古屋大学大型計算機センターニュース, Vol.28, No.4, 280-291, 1997.
[7] 荻野竜樹、「コンピュータシミュレーションと可視化」,
愛媛大学総合情報処理センター広報, Vol.6, 4-15, 1999.
http://gedas.stelab.nagoya-u.ac.jp/simulation/simua/ehime985.html
[8] 荻野竜樹,「VPP FortranからHPFへ」,名古屋大学大型計算機センターニュース 解説,
372-405, Vol.31, No.4, (2000).
http://gedas.stelab.nagoya-u.ac.jp/simulation/hpfja/hpf013.html
[9] Ogino, T., Global MHD Simulation Code for the Earth's Magnetosphere Using HPF/JA,
Special Issues of Concurrency: Practice and Experience, 14, 631-646, 2002.
http://gedas.stelab.nagoya-u.ac.jp/simulation/hpfja/mhd00.html
[10] 津田知子、「新スーパーコンピュータVPP5000/56の利用について」、
名古屋大学大型計算機センターニュース、Vol.31, No.1, 18-33, 2000.
[11] 津田知子、「MPIによる並列化」、名古屋大学情報連携基盤センター MPI講習会資料、
2002年2月
[12] High Performance Fortran Forum, 「High Performance Fortran 2.0 公式マニュアル」、
Springer, 1999.
[13] 富士通株式会社、「HPFプログラミング 〜並列プログラミング(HPF編)
UXP/V 第1.0 版、2000年6月.
[14] 富士通株式会社、「VPP FORTRANプログラミング」、UXP/V, UXP/M
第1.2版、1997年4月.
[15] 富士通株式会社、「MPIプログラミング 〜Fortran, C〜」第1.3版、2001年4月.
[16] 富士通株式会社、「MPI使用手引き書 V20用」、UXP/V 初版 1999年9月
[17] 青山幸也(日本アイ・ビーエム株式会社)、「並列プログラミング虎の巻 MPI版」
虎の巻シリーズ2、2001年1月.
[18] 株式会社日立製作所、「スーパーテクニカルサーバSR8000プログラム移植報告書」
国立極地研究所、2002年3月.
[19] 名古屋大学情報連携基盤センター、「スーパーコンピュータVPP5000利用の手引き」
2002年4月.
「VPP5000利用の手引きのpdfファイル」
http://nucc.cc.nagoya-u.ac.jp/CENT/vpp_tebiki.pdf
「スーパーコンピュータ VPP5000/64 利用案内」のHomepage
http://www2.itc.nagoya-u.ac.jp/sys_riyou/vpp/vpptebiki.htm
図1.3次元MHDシミュレーションに用いる太陽地球磁気圏座標系
Fig.1 Solar-terrestrial magnetosphere coordinate system in the 3-dimensional MHD simulation.
図2.Modified Leap-Frog法の計算スキーム
Fig.2 Diagram of Modified Leap-Frog numerical scheme.
図3.Modified leap-frog法(MLF)、2 step Lax-Wendroff法(2LW)及びRunge-Kutta-Gill法(RKG)に対する増幅率の絶対値と位相速度の波数依存性
Fig.3 Dependency of the absolute value and phase velocity of the amplification factor on wave number in cases of modified leap-frog,2 step Lax-Wendroff and Runge-Kutta-Gill methods.
図4.
l を変化したときのModified leap-frog法(MLF)に対する増幅率の絶対値と位相速度の波数依存性
Fig.4 Dependency of the absolute value and phase velocity of the amplification factor on wave number for modified leap-frog method with different l values.
図5.3種類の計算方法を用いた波動方程式のシミュレーション
Fig.5 Simulation of the wave equation for 3 different kinds of numerical schemes.
図6.3種類の計算方法を用いたMHD衝撃波のシミュレーション
Fig.6 Simulation of the MHD shock wave for 3 different kinds of numerical schemes.
図7.太陽と地球を結ぶ子午面と赤道面の地球磁気圏の構造と磁気圏尾部の断面図(白黒図:gm150b.ps)
Fig.7 Magnetospheric configurations in the noon-midnight meridian and equator and cross sectional patterns (black and white:gm150b.ps).
図8.太陽と地球を結ぶ子午面と赤道面の地球磁気圏の構造と磁気圏尾部の断面図(カラー図:gm220b.ps)
Fig.8 Magnetospheric configurations in the noon-midnight meridian and equator and cross sectional patterns (color:gm220b.ps).
図9.地球磁気圏の磁力線の3次元構造(gm480b.ps)
Fig.9 3-dimensional configuration of magnetic field lines in the earth's magnetosphere.
図10.VRMLを用いた地球磁気圏のの可視化(zvrml01.wrl)
Fig.10 3-dimensional visualization of the earth's magnetosphere by using VRML.