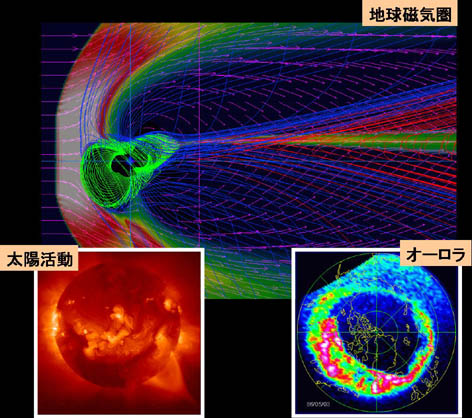
図1 太陽活動とジオスペース(地球外圏)環境変化の因果関係を調べる太陽風と地球磁気圏相互作用
名古屋大学太陽地球環境研究所 荻野竜樹 名古屋大学情報連携基盤センター 津田知子
1.はじめに
太陽観測衛星「ようこう」の軟X線画像が明らかにしたように、太陽活動は時々刻々大きく変動しており、その影響として地球磁気圏電離圏ではサブストーム/磁気嵐が発生し、極地方では活発なオーロラがみられる。その太陽活動とジオスペース(地球外圏)環境変化の因果関係を解明しようとするのが、図1に示す太陽風と地球磁気圏相互作用の研究である。太陽風と地球磁気圏相互作用の3次元グローバル電磁流体力学的(MHD)シミュレーションは、約25年前に、力が釣り合った平均的な磁気圏の形をやっと再現できるところから出発して、コンピュータとIT技術の長足の進歩に相まって発展を続け、最近では、衛星・地上観測と比較して磁気圏のダイナミックスを議論できる程度にまで成長してきた。こうして、上流の太陽風や惑星間磁場(IMF)の変化に対する磁気圏・電離圏の応答や、磁気圏での大きな擾乱現象であるサブストームや磁気嵐を直接シミュレーションから調べようとする試みも行われるようになってきた。これらの太陽風磁気圏相互作用のグローバルMHDシミュレーションを精度よく実行するためには、外部境界をできるだけ遠くに設定してかつ空間分解能をできるだけ上げることが望ましい点から、計算方法の改良が一方で必要であると同時に、最大級のスーパーコンピュータの利用、それも効率的な並列計算法の利用は不可欠である。

図1 太陽活動とジオスペース(地球外圏)環境変化の因果関係を調べる太陽風と地球磁気圏相互作用
そのような並列計算共通プログラム言語の候補として、High Performance Fortran (HPF)とMessage Passing Interface(MPI)がある。HPFは、米国の共同研究者が共通プログラム言語として優れていると言っている反面、多くの大型プログラムで性能が十分に出ないという欠点が指摘されていた。こうした中、2000年からHPF/JA(JAHPFによるHPFの日本拡張版)が使えるようになり、VPP Fortranでフルベクトル化フル並列化されている流体コードやMHDコードは、比較的容易にHPF/JAに書き換えることができて、更にそのHPF/JA のプログラムはVPP Fortranと同等の性能を得ることができるようになった。しかし、HPF/JAの成功にもかかわらず、HPFの普及は進んでいないのが現状である。そして、世界標準並列化手法として最後に残ったMPIに対する期待が高まっていた。この VPP FortranとHPF/JAからMPIへの書き換えもMHDモデルでは上手くことが運び、VPP5000では3者とも高効率の並列計算を実現できるようになった。
しかし、富士通株式会社のスーパーコンピュータもベクトル並列機の開発はVPP5000で終了し、後継機種はクラスター型のスカラー並列機PRIMEPOWER HPC2500になる。超並列機の性能は全く予断を許さない。米国では通常の並列プログラムに対する最大規模の超並列機の効率は3-7%とも言われており、またDOEのスーパーコンピュータ利用科学研究マネージャーの超並列機の効率予測は最大10%となっている。このように、ベクトル並列機が30-70%の高効率を実現してきたのに対して、大規模の超並列機は大体10%以下の効率しか実現できていない。この高効率並列計算を実現できるかどうかが、大規模の計算が必要なシミュレーション研究者にとって、VPP5000からPRIMEPOWER HPC2500の移行に対する最大の心配ごとであった。こうして、クラスター型のスカラー並列機PRIMEPOWER HPC2500の性能を実用的グローバル3次元MHDコードを用いて調べることにした。
2.地球磁気圏の3次元グローバルMHDモデル
太陽風磁気圏相互作用の3次元MHDモデルでは、MHD方程式とマックスウェル方程式を初期値境界値問題として、様々な方法でその時間発展を解いている。偏微分方程式を差分化して2 step Lax-Wendroff法で解く方法などはその例である。空間分解能を上げるための計算方法における様々な工夫として、非一様格子法、非構造格子法、自動調節格子法、時空間多重格子法の導入などが行われている。私達は、高精度計算法の一つであるmodified leap-frog 法を用いた3次元グローバルMHDシミュレーションから、太陽風や惑星間磁場(IMF)の変化に依存した地球磁気圏電離圏の応答を調べている。
MHDモデルの基礎となる規格されたMHD方程式とMaxwell方程式を以下に示す。
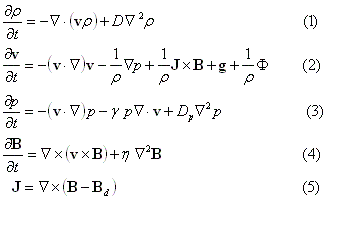
式(1)〜(4)はそれぞれ、連続の式、運動方程式、エネルギー保存則より求まる圧力変化の式、インダクション方程式と呼ばれる磁場変化を示す式である。ただし、ρはプラズマ密度、vは速度ベクトル、pはプラズマ圧力、Βは磁場ベクトルである。この8つのパラメータを未知数として求めていく。ただし、差分法の数値誤差により、Βdに対するJが本来の零とは違って有限値になるため、式(5)を用いてその数値誤差を除去している。ここでのΒdは地球の固有磁場としての双極子磁場である。
シミュレーションには、図2に示すような太陽方向x軸正、夕方向y軸正、磁気北極方向z軸正とした太陽地球磁気圏座標系を用いて、MHD方程式とマックスウェル方程式を時空間で差分化し、初期値境界値問題としてMHD方程式の8個の物理変数の時間発展を解く。ここでは、朝夕と南北で対称性を仮定した1/4領域の地球磁気圏モデルを示している。シミュレーションで用いるmodified leap-frog法は、two step Lax-Wendroff法の数値的安定化効果を一部取り入れて、leap-frog法の数値的減衰と分散の小さい効果をより多く取り入れた、数値的減衰と分散にバランスの良くとれた一種の組み合わせ計算方法となっている。また、パラメータを変化させることによって、性質の良く分かった2つの計算方法に一致させることができるので、結果に与える数値誤差の影響も理解し易い利点を持っている。3次元MHDコードのフローチャートを図3に示す。計算環境設定のパラメータを与えて、初期値を決め、計算継続の場合は前のデータを読み込んで、2段解法のmodified leap-frogスキームを開始する。並列計算では、z方向に領域分割しているので領域分割間データの転送が必要である。そのデータ転送も図3に示すように、必要最小限の2カ所にコンパクトにまとめてある。
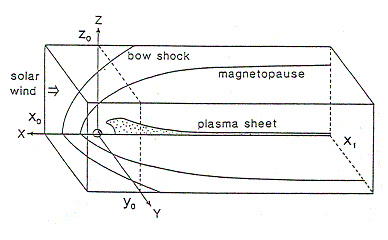 | 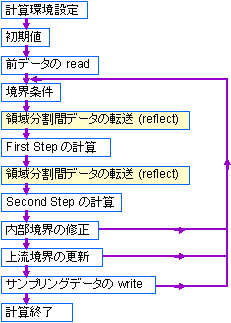 | |
| 図2 3次元MHDシミュレーションに用いる太陽地球磁気圏座標系 | 図3 3次元MHDコードのフローチャート |
スーパーコンピューティングの説明に進む前に、太陽地球磁気圏相互作用の3次元グローバルMHDシミュレーションの例を図4と図5に示す。図4は磁気軸が30度傾いている北半球が夏の場合、惑星間磁場(IMF)の南北向きの違いによる地球磁気圏構造の違いを磁力線とプラズマ温度分布で示す。南向きIMFでは磁気圏尾部の磁力線が直線的形状になって薄いプラズマシートが形成されているのに対し、北向きIMFでは磁力線が丸い形状になって厚いプラズマシートが形成されているのがみられる。このように、惑星間磁場が南北に向きを変える時、磁気圏の形は大きく変化し、それがIMFと地球磁場の間の磁気リコネクションの起こり方の違いによることが理解される。図5は、衛星観測の太陽風と惑星間磁場データを計算のインプットとして用いた場合、1999年10月の大きな磁気嵐に対するMHDシミュレーション結果で、磁気嵐前と磁気嵐時の磁気圏構造の変化を示している。磁気嵐前はIMFが北向きであったために丸い形状の磁力線が広がっているが、磁気嵐時には丸い形状(ダイポール型)の磁力線は地球近傍に収縮して、静止衛星軌道(6.6Re)より内側で丸い形状(ダイポール型)から直線的形状(テール型)に急激に遷移している。このように、3次元グローバルMHDシミュレーションから、太陽風と惑星間磁場の変化に対する地球磁気圏の応答を知ることができる。
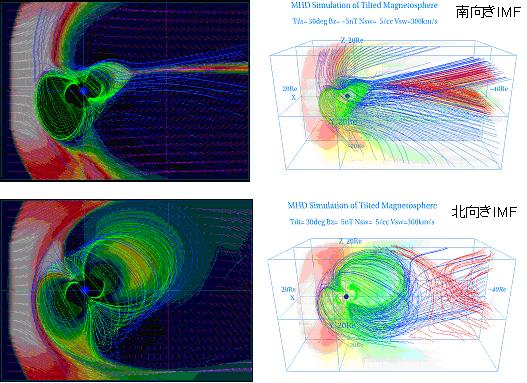
図4 磁気軸が傾いている場合で、惑星間磁場(IMF)の南北向きの違いによる地球磁気圏構造の変化
 |  |
3.VPPにおける並列化
1995年にFujitsu VPP500が使用できるようになって、太陽風と地球磁気圏相互作用のグローバルMHDシミュレーションを実行するためのフルベクトル化されていた3次元MHDコードをVPP Fortran用に書き換えた。コードの全面的な書き換えを行って、VPP Fortranで計算効率の高い、ほぼフルベクトル化フル並列化された3次元MHDコードを作成した[荻野、1997]。その後、2000年に3次元MHDコードをVPP FortranからHPF/JAへ書き換えた[荻野、2000; Ogino, 2002]。結果的には、HPF/JAで書いた3次元MHDコードもVPP Fortranの3次元MHDコードと同様にフルベクトル化フル並列化することができ、計算速度もVPP Fortranと同等の性能を得ることができた。VPP Fortranでも、HPF/JAでもベクトル並列化MHDコードとしては、ほとんど同等のものであるが、ベクトル化MHDコードとは全く別物である。その最も大きな違いは、ベクトル化MHDコードは、プログラムサイズを最小化しているのに対し、ベクトル並列化MHDコードでは並列計算の性質上プログラムサイズの最小化が不可能だったことである。このため、同じ格子点数のMHDシミュレーションをする場合、ベクトル化コードに比べて、ベクトル並列化コードは約3〜4倍のコンピュータメモリが必要となった[荻野、2000; Ogino, 2002]。
2002年になって、周りの人の協力を得てHPF/JAからMPIへとVPP FortranからMPIへの書き換えを行い、MPIでほぼフルベクトル化フル並列化された3次元MHDコードを作成することができた。その計算速度は、VPP FortranやHPF/JAのMHDコードと同等以上の高計算効率を得ることができた。書き換えの労力だが、VPP FortranやHPF/JAでフルベクトル化フル並列化された3次元MHDコードがあれば比較的容易にMPI利用のFortranコードに書き換えることが可能である。実際、プログラムの構造をほとんど変えずに、VPP FortranとHPF/JAからMPIの並列化指示行を挿入することでプログラムの大半の部分を書き換えることができる。それに、それぞれのコンパイラーに特有の部分をユニットとして追加すれば、プログラムの大部分ができあがる。後に残される問題は、大まかに言えば境界条件と入出力である。これらも通常の場合はそれほど深刻な問題とはならない。しかし、MPIで超大型計算まで目標としている場合には、境界条件と入出力には注意が必要である。
ベクトル化や並列化した場合、非ベクトル化コードや非並列化コードに比べて何倍の速度向上率が得られるかを示すものに、アムダールの法則がある。その法則によると、多数のPE(Processing Element)を用いて高い速度向上率を得るためには、並列化率が100%に限りなく近いことが極めて重要となる。従って、高効率のシミュレーションコードを作成するためには、どうやってフルベクトル化とフル並列化を実現するかにかかっている。実際には、内側のdo loopでベクトル化されているので、そのベクトル化を維持したまま外側のdo loopで並列化をすればよいことになる。よく、「計算時間のかかっているdo loopから並列化せよ」と言われるが、その方法だとある程度までは並列化効率が上がるが、100%に近い並列化効率を得ることはほとんど不可能である。これまでのベクトル化と並列化の経験からすると、プログラムの構造をきちんと決めることが最も重要であると確信している。分散メモリ型並列計算機を用いる場合の並列計算の基本は単純なことで、計算する前に計算に必要な変数を全て各PEに集めればよいわけで、それもできるだけ一括して転送し、転送回数をできるだけ少なくすればよい。即ち、プログラムの構造とは、領域分割の変数(方向)を軸とした計算の流れを示すフローチャートに、効率的な配列の利用内容を割り付けたものである。並列計算プログラムでは通常作業配列を多く取る必要が生じるので、プログラムの構造を決める時に作業配列の量を最小にすることが同時に必要となる。
4.PRIMEPOWER HPC2500 (ngrd)における並列化
3次元グローバルMHDコードは、VPPで使用していたMPIバージョンのプログラムをほとんどそのまま使用していて、VPPの場合と同じようにk (z)方向のみに1次元の領域分割を行って、数値計算法としてはModified leap-frog法を用いている。従って、配列の順序は、f(nx2,ny2,nz2,nb)のように、x方向、y方向、z方向、8個のMHD方程式の成分の順序である。
次に、PRIMEPOWER HPC2500で使用し、現在までで最高の計算速度を出した3次元MHDコードの最終MPIバージョンの重要な部分を示す。先ず、f(nx2,ny2,nz2,nb)からF(nb,nx2,ny2,nz2)への配列の順序の並び替えを宣言している。これは差分で解くため、MHD方程式の8成分は近傍の格子点で必ず値を参照されるので、遠くに離さない方がよいためである。z方向の分割はMPIで標準的な連続領域分割を用いる。また、VPP Fortranの袖あるいはHPF/JAのreflectとして用いていた、領域分割の両端のデータをcpu間で通信する場合は、次に示す様にwild card、mpi_sendrecvの利用及び通信データのコンパクト化を行っている。
<< MPIバージョンの3次元グローバルMHDコード >>
#define f(a,b,c,d) F(d,a,b,c)
#define ff(a,b,c,d) FF(d,a,b,c)
#define p(a,b,c,d) P(d,a,b,c)
#define u(a,b,c,d) U(d,a,b,c)
c
parameter (npe=48)
integer recvcount(npe),displs(npe)
c
parameter (nx=500,ny=318,nz=318,nxp=150,nb=8)
parameter (nx2=nx+2,ny2=ny+2,nz2=nz+2)
parameter (nzz=(nz2-1)/npe+1)
dimension f(nx2,ny2,0:nzz+1,nb),u(nx2,ny2,0:nzz+1,nb)
c
!hpf$ reflect f
CC MPI START
iright = irank + 1
ileft = irank - 1
if(irank.eq.0) then
ileft = MPI_PROC_NULL
else if(irank.eq.isize-1) then
iright = MPI_PROC_NULL
end if
do m=1,nb
ftemp1=f(:,:,ks,m)
ftemp2=f(:,:,ke+1,m)
call mpi_sendrecv(ftemp1,n2,mpi_real,ileft,100,
& ftemp2,n2,mpi_real,iright,100,
& mpi_comm_world,istatus,ier)
f(:,:,ks,m)=ftemp1
f(:,:,ke+1,m)=ftemp2
end do
CC MPI END
名古屋大学情報連携基盤センターに2002年度に導入された富士通のクラスター型スカラー並列機
PRIMEPOWER HPC2500 (ngrd) の性能を次に示す。
<< 名古屋大学情報連携基盤センターのPRIMEPOWER HPC2500 (ngrd) の性能 >>
【CPU】
32CPU構成×2筐体=計64CPU
(このうち、Batchには24CPU×2を使用、あとは、TSSとGrid用)
・SPARC64 V(1.3GHz)
・内部キャッシュ(1次キャッシュ:命令128KB+データ128KB、2次キャッシュ:2MB)
・理論計算速度:5.2 GFlops/CPU, 332.8 GFlops/TOTAL
【メモリ】
64GB×2筐体=計128GB
【高速インターコネクト】
ノード間通信性能:4GB/s×2=8GB/s (理論性能値)
・33CPU以上ではGbEを使用
次に、PRIMEPOWER HPC2500で3次元MHDコードをコンパイルした時のオプションと実行シェルを示す。最高速の計算結果は最後のコンパイルオプションで実現した。このオプションでは、キャッシュのレベルの最適化、largepageの利用、64bit対応用のオプションV9のオフを採用している。実行シェルも最高速の計算結果を得た時のものである。
<< PRIMEPOWER HPC2500 (ngrd) でのコンパイルオプションと実行シェル >> mpifrt -KV9 -o progmpi progmpi.f mpifrt -Kfast_GP2=3 -o progmpi progmpi.f mpifrt -Kfast_GP2=3,largepage=2 -o progmpi progmpi.f mpifrt -Kfast_GP2=3,largepage=2 -o progmpi progmpi.f mpifrt -Kfast_GP2=3,V9 -O5 -Kprefetch=4,prefetch_cache_level=2,prefetch_strong -o progmpi progmpi.f mpifrt -Kfast_GP2=3,largepage=2,V9 -O5 -Kprefetch=4,prefetch_cache_level=2,prefetch_strong -o progmpi progmpi.f mpifrt -Kfast_GP2=3,largepage=2,V9 -O5 -Kprefetch=4,prefetch_cache_level=2,prefetch_strong -Cpp -o progmpi progmpi.f mpifrt -Kfast_GP2=3,largepage=2 -O5 -Kprefetch=4,prefetch_cache_level=2,prefetch_strong -Cpp -o progmpi progmpi.f qsub mpiexec.sh ngrd% more mpiexec.sh # @$-q gs -eo -o mpiexec.out # @$-lP 16 -lM 3.0gb -ls 128mb mpiexec -n 16 -mode limited ./mearthd2/progmpi
5.HPC2500 (ngrd)とVPPにおける3次元MHDコード計算速度
3次元MHDシミュレーションなどの大型シミュレーションを実行するためには、スーパーコンピュータの利用と、ベクトル化や並列化による計算速度の効率化は必須である。表1に、富士通VPP5000/64を用いて、VPP Fortran、HPF/JA及びMPIで書かれた3次元MHDコードを実行した場合の計算処理速度の比較を示す。計算時間(sec)は、Modified leap-frog法で1回時間ステップを進めるのに要する時間を示している。VPP Fortran, HPF/JA及びMPIで同等の計算速度がでていて、スケーラビリティも良くかつその計算効率もかなり高いことが分かる。これらの並列計算MHDコードはフルベクトル化とフル並列化ができていて、VPP FortranとHPF/JAとMPIのいずれの大規模計算でも400 Gflops程度以上の高効率も実現している。
表2に、HPC2500(ngrd)とVPP5000/64を用いて、MPIとHPF/JAで書かれた3次元グローバルMHDコードを実行した場合の計算処理速度の比較を示す。実際の太陽風地球磁気圏相互作用の3次元MHDシミュレーションでは、約1万回以上の繰り返し計算をするので、大規模計算になるとVPP5000でも100時間のオーダーの計算時間がかかる。VPP5000利用のMPIとHPF/JAの3次元MHDコードでの格子点数は、境界を除いて(nx,ny,nz)=(500,318,318)である。領域分割の両端のデータをcpu間で通信する方法としてHPF/JAではreflectの一通りに対して、MPIではmpi_send and mpi_recv、mpi_isend and mpi_irec、mpi_sendrecvの3つの方法があるが、その3者の間の差異はほとんどみられない。また、計算は正しくないが比較のために、領域分割の両端のデータ通信を停止した場合の計算速度も測定した。その通信を停止した場合の計算速度に対する通信有りの計算速度の比は、HPF/JAで81.7%、MPIで90.5%であった。
HPC2500(ngrd)は、他との差異は少なかったのでMPIでのmpi_sendrecvを利用した結果のみを示す。コンパイルオプションは(nx,ny,nz)=(250,158,158)では2番目、(500,318,318)では最後の最高速の計算結果を得た場合である。32cpuまではかなりよいスケーラビィリティが得られている。多くの格子点(500,318,318)の使用では、配列の順序の並び替えf(nb,nx2,ny2,nz2)を宣言して、かつlargepageを使用している。また、33cpu使用で計算速度が急に遅くなっているのは、HPC2500(ngrd)において33cpu以上では高速ネットワークが働かなくなるからである。通信停止の場合の計算速度を測定すると48cpuまで確実によいスケーラビィリティが得られている。その通信を停止した場合の計算速度に対する通信有りの計算速度の比は、32cpuで76.9%であった。(nx,ny,nz)=(500,318,318)の格子点を用いた場合、VPP5000の1cpuでの速度6.90 Gflopsに対して、HPC2500 (ngrd)の8cpuで8.36 Gflopsの計算速度を得ているように、VPP5000の1cpuに対してHPC2500 (ngrd)の7cpuで同等の速度を得ることができる。この結果は他の高効率計算の例と同様の結果を示している。
表1 名古屋大学情報連携基盤センターの富士通VPP5000/64を用いて、VPP Fortran、HPF/JA及びMPIで書かれた太陽風と地球磁気圏相互作用の3次元グローバル電磁流体力学的(MHD)コードで調べた場合の計算処理速度の比較。
Table 1. Comparison of computer processing capability between VPP Fortran, HPF/JAand MPI in a 3-dimensional global MHD code of the solar wind-magnetosphere interaction by using Fujitsu VPP5000/64.
Number Number of VPP Fortran HPF/JA MPI
of PE grids cpu time Gflops Gf/PE cpu time Gflops Gf/PE cpu time Gflops Gf/PE
1PE 200x100x478 119.607 ( 0.17) 0.17 (scalar)
1PE 200x100x478 2.967 ( 6.88) 6.88 3.002 ( 6.80) 6.80
2PE 200x100x478 1.458 ( 14.01) 7.00 1.535 ( 13.30) 6.65 1.444 ( 14.14) 7.07
4PE 200x100x478 0.721 ( 28.32) 7.08 0.761 ( 26.85) 6.71 0.714 ( 28.60) 7.15
8PE 200x100x478 0.365 ( 55.89) 6.99 0.386 ( 52.92) 6.62 0.361 ( 56.55) 7.07
16PE 200x100x478 0.205 ( 99.38) 6.21 0.219 ( 93.39) 5.84 0.191 (107.19) 6.70
24PE 200x100x478 0.141 (144.49) 6.02 0.143 (143.02) 5.96 0.1302(157.24) 6.55
32PE 200x100x478 0.107 (191.23) 5.98 0.110 (186.13) 5.82 0.1011(202.50) 6.33
48PE 200x100x478 0.069 (297.96) 6.21 0.074 (276.96) 5.77 0.0679(301.51) 6.28
56PE 200x100x478 0.064 (319.53) 5.71 0.068 (299.27) 5.34 0.0639(320.39) 5.72
64PE 200x100x478 0.0662(308.91) 4.83 0.0627(324.57) 5.07 0.0569(359.80) 5.62
1PE 500x100x200 2.691 ( 7.94) 7.94 2.691 ( 7.94) 7.94
2PE 500x100x200 1.381 ( 15.47) 7.73 1.390 ( 15.37) 7.68 1.357 ( 15.74) 7.87
4PE 500x100x200 0.715 ( 29.97) 7.47 0.712 ( 29.99) 7.50 0.688 ( 31.03) 7.76
8PE 500x100x200 0.398 ( 53.65) 6.71 0.393 ( 54.38) 6.80 0.372 ( 57.50) 7.19
16PE 500x100x200 0.210 (101.87) 6.37 0.202 (105.74) 6.61 0.193 (110.70) 6.92
24PE 500x100x200 0.160 (133.70) 5.57 0.150 (142.40) 5.93 0.135 (158.26) 6.59
32PE 500x100x200 0.131 (163.55) 5.11 0.120 (175.50) 5.48 0.1084(197.10) 6.15
48PE 500x100x200 0.100 (214.48) 4.46 0.091 (231.69) 4.82 0.0811(263.44) 5.49
56PE 500x100x200 0.089 (239.48) 4.28 0.086 (244.85) 4.37 0.0688(310.54) 5.55
64PE 500x100x200 0.0956(222.95) 3.48 0.0844(249.49) 3.90 0.0687(310.99) 4.86
2PE 800x200x478 10.659 ( 15.33) 7.66 10.742 ( 15.21) 7.60 10.428 ( 15.67) 7.83
4PE 800x200x478 5.351 ( 30.53) 7.63 5.354 ( 30.52) 7.63 5.223 ( 31.28) 7.82
8PE 800x200x478 2.738 ( 59.67) 7.46 2.730 ( 59.85) 7.48 2.696 ( 60.61) 7.58
12PE 800x200x478 1.865 ( 87.58) 7.30 1.911 ( 85.49) 7.12 1.771 ( 92.25) 7.68
16PE 800x200x478 1.419 (115.12) 7.19 1.389 (117.66) 7.35 1.342 (121.81) 7.61
24PE 800x200x478 0.975 (167.54) 6.98 0.976 (167.45) 6.98 0.905 (180.59) 7.52
32PE 800x200x478 0.722 (226.33) 7.07 0.717 (227.72) 7.12 0.690 (236.63) 7.39
48PE 800x200x478 0.534 (305.70) 6.36 0.515 (317.26) 6.61 0.469 (348.38) 7.25
56PE 800x200x478 0.494 (330.95) 5.91 0.464 (352.49) 6.29 0.433 (377.73) 7.74
64PE 800x200x478 0.465 (351.59) 5.49 0.438 (373.41) 5.83 0.389 (420.45) 6.57
4PE 800x200x670 7.618 ( 30.06) 7.52 8.001 ( 28.62) 7.16 7.433 ( 30.81) 7.70
8PE 800x200x670 3.794 ( 60.36) 7.54 3.962 ( 57.81) 7.23 3.683 ( 62.17) 7.77
12PE 800x200x670 2.806 ( 81.61) 6.80 3.005 ( 76.21) 6.35 2.696 ( 84.95) 7.08
16PE 800x200x670 1.924 (119.00) 7.44 2.012 (113.85) 7.12 1.854 (123.53) 7.72
24PE 800x200x670 1.308 (175.10) 7.30 1.360 (168.44) 7.02 1.254 (182.61) 7.60
32PE 800x200x670 0.979 (233.85) 7.31 1.032 (221.88) 6.93 0.955 (239.77) 7.49
48PE 800x200x670 0.682 (335.62) 6.99 0.721 (317.80) 6.62 0.662 (346.21) 7.21
56PE 800x200x670 0.595 (384.61) 6.87 0.628 (364.87) 6.52 0.572 (400.59) 7.15
64PE 800x200x670 0.519 (441.50) 6.90
16PE 1000x500x1118 9.668 (123.52) 7.72 9.619 (125.50) 7.84
32PE 1000x500x1118 5.044 (236.73) 7.40 4.992 (241.83) 7.56
48PE 1000x500x1118 3.550 (336.40) 7.01 3.479 (346.97) 7.23
56PE 1000x500x1118 2.985 (400.04) 7.14 2.935 (411.36) 7.35
32PE 1000x1000x1118 9.979 (239.33) 7.48 9.813 (243.37) 7.61
48PE 1000x1000x1118 7.177 (332.79) 6.93 7.028 (339.85) 7.08
56PE 1000x1000x1118 5.817 (410.55) 7.33 5.794 (412.23) 7.36
------------------------------------------------------------------------
: Mflops is an estimated value in comparison with the computation by
1 processor of CRAY Y-MP C90.
表2 名古屋大学情報連携基盤センターの富士通HPC2500(ngrd)とVPP5000/64を用いて、MPIとHPF/JAで書かれた太陽風と地球磁気圏相互作用の3次元グローバル電磁流体力学的(MHD)コードで調べた場合の計算処理速度の比較。
Table 2. Comparison of computer processing capability in the MPI and HPF/JA 3-dimensional global MHD codes of the solar wind-magnetosphere interaction by using Fujitsu HPC2500 and VPP5000/64. The used 3D MHD code is to solve full 3D Earth's Magnetosphere with grid points of (nx,ny,nz)=(250,158,158) and (500,318,318).
Kind of Number of cpu time Gflops Gf/PE cpu time Gflops Gf/PE Date
computer PEs (sec) (sec)
------------------------------------------------------------------------------------
HPF/JA reflect MPI mpi_send and mpi_recv
VPP5000 1PE 16.7886 ( 6.44) 6.44
VPP5000 2PE 8.3927 ( 12.87) 6.44 7.8305 ( 13.80) 6.90
VPP5000 4PE 4.4073 ( 24.52) 6.13 4.0589 ( 26.61) 6.65
VPP5000 8PE 2.1753 ( 49.67) 6.21 1.9973 ( 54.10) 6.76
VPP5000 16PE 1.1446 ( 94.40) 5.90 1.0103 ( 106.95) 6.68
VPP5000 32PE 0.6139 ( 176.01) 5.50 0.5116 ( 211.21) 6.60
MPI mpi_sendrecv MPI mpi_isend and mpi_irecv
VPP5000 2PE 7.8334 ( 13.79) 6.90 7.8227 ( 13.81) 6.90
VPP5000 16PE 1.0109 ( 106.88) 6.68
VPP5000 32PE 0.5127 ( 210.74) 6.59 0.5089 ( 212.31) 6.63
HPF/JA without comm MPI without comm
VPP5000 2PE 7.8898 ( 13.69) 6.85 7.3934 ( 14.61) 7.31
VPP5000 32PE 0.5016 ( 215.40) 6.73 0.4639 ( 232.90) 7.28
------------------------------------------------------------------------------------
MPI
HPC2500 (ngrd) 2PE (250,158,158) sendrecv -KV9 6.7873 ( 1.999) 0.999
HPC2500 (ngrd) 4PE (250,158,158) sendrecv -KV9 3.5883 ( 3.780) 0.945
HPC2500 (ngrd) 8PE (250,158,158) sendrecv -KV9 1.8780 ( 7.224) 0.903
HPC2500 (ngrd) 16PE (250,158,158) sendrecv -Kfast 0.8991 ( 15.091) 0.943
HPC2500 (ngrd) 24PE (250,158,158) sendrecv -Kfast 0.6378 ( 21.273) 0.886
HPC2500 (ngrd) 32PE (250,158,158) sendrecv -Kfast 0.5036 ( 26.940) 0.841
HPC2500 (ngrd) 48PE (250,158,158) sendrecv -Kfast 4.8827 ( 2.779) 0.058
HPC2500 (ngrd) 2PE (250,158,158) no comm -KV9 6.7865 ( 1.999) 0.999
HPC2500 (ngrd) 4PE (250,158,158) no comm -KV9 3.3942 ( 3.997) 0.999
HPC2500 (ngrd) 8PE (250,158,158) no comm -KV9 1.7190 ( 7.892) 0.986
HPC2500 (ngrd) 16PE (250,158,158) no comm -Kfast 0.8289 ( 16.366) 1.023
HPC2500 (ngrd) 24PE (250,158,158) no comm -Kfast 0.5898 ( 23.001) 0.958
HPC2500 (ngrd) 32PE (250,158,158) no comm -Kfast 0.4464 ( 30.387) 0.950
HPC2500 (ngrd) 48PE (250,158,158) no comm -Kfast 0.3755 ( 36.125) 0.753
HPC2500 (ngrd) 2PE (500,318,318) sendrecv -Cpp 48.4191 ( 2.231) 1.116
HPC2500 (ngrd) 4PE (500,318,318) sendrecv -Cpp 24.7140 ( 4.372) 1.093
HPC2500 (ngrd) 8PE (500,318,318) sendrecv -Cpp 12.9242 ( 8.360) 1.045
HPC2500 (ngrd) 16PE (500,318,318) sendrecv -Cpp 6.8664 ( 15.736) 0.983
HPC2500 (ngrd) 20PE (500,318,318) sendrecv -Cpp 5.6745 ( 19.041) 0.952
HPC2500 (ngrd) 24PE (500,318,318) sendrecv -Cpp 4.9517 ( 21.820) 0.909
HPC2500 (ngrd) 32PE (500,318,318) sendrecv -Cpp 4.1945 ( 25.760) 0.805
HPC2500 (ngrd) 33PE (500,318,318) sendrecv -Cpp 15.2646 ( 7.078) 0.214
HPC2500 (ngrd) 40PE (500,318,318) sendrecv -Cpp 13.9701 ( 7.733) 0.193
HPC2500 (ngrd) 48PE (500,318,318) sendrecv -Cpp 12.5962 ( 8.577) 0.179
HPC2500 (ngrd) 2PE (500,318,318) no comm -Cpp 47.6551 ( 2.268) 1.134
HPC2500 (ngrd) 4PE (500,318,318) no comm -Cpp 22.6370 ( 4.774) 1.194
HPC2500 (ngrd) 8PE (500,318,318) no comm -Cpp 11.6999 ( 9.237) 1.155
HPC2500 (ngrd) 16PE (500,318,318) no comm -Cpp 5.8821 ( 18.376) 1.148
HPC2500 (ngrd) 24PE (500,318,318) no comm -Cpp 4.3032 ( 25.118) 1.047
HPC2500 (ngrd) 32PE (500,318,318) no comm -Cpp 3.2285 ( 33.479) 1.046
HPC2500 (ngrd) 48PE (500,318,318) no comm -Cpp 2.3294 ( 46.401) 0.967
------------------------------------------------------------------------------------
6.計算速度の比較の考察と問題点
HPC2500(ngrd)とVPP5000/64を用いて、MPIとHPF/JAで書かれた3次元グローバルMHDコードを実行した場合の計算処理速度の比較を表1、2からグラフにして図6−9に示す。HPC2500(ngrd)におけるcpu数を増加した時のスケーラビィリティの良さが明瞭にみられる。図6のVPP5000によるVPP Fortran、HPF/JA及びMPIで書かれた3次元MHDコードの計算処理速度の比較では3つとも同程度であるが、小さな差異をみるとMPI が一番速く、HPF/JA、VPP Fortranの順に計算速度が少し遅くなっている。図7は、HPC2500との比較のために格子点数が(nx,ny,nz)= (500,318,318)の場合を示した。図8と図9は格子点数が(nx,ny,nz)=(250,158,158)と(500,318,318)の場合に対するHPC2500での計算速度を示し、32cpuまでスケーラビィティがよいのが分かる。33cpu以上では計算速度が急に低下している。
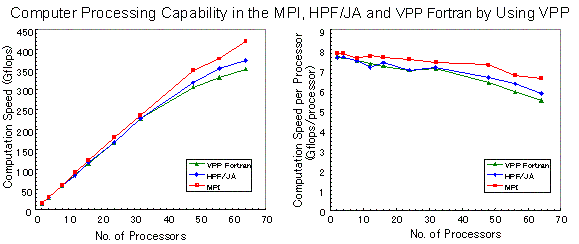
図6 VPP5000によるVPP Fortran、HPF/JA及びMPIで書かれた3次元MHDコードの計算処理速度の比較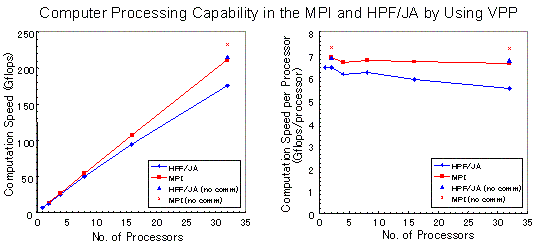
図7 VPP5000によるMPIとHPF/JAで書かれた3次元MHDコード
の計算処理速度の比較、格子点数は(nx,ny,nz)=(500,318,318)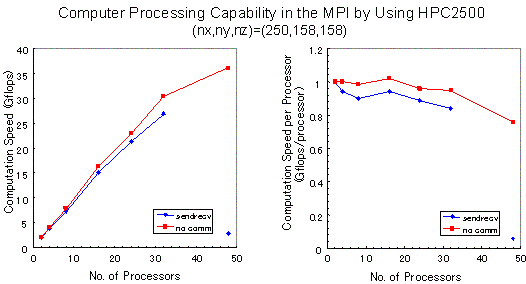
図8 HPC2500によるMPIのMHDコードの計算処理速度、格子点数は(nx,ny,nz)=250,158,158)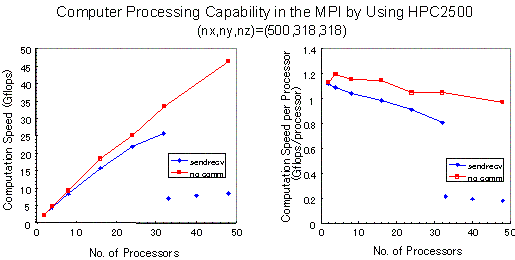
図9 HPC2500によるMPIのMHDコードの計算処理速度、格子点数
は(nx,ny,nz)=(500,318,318)
PRIMEPOWER HPC2500で、33cpu以上では並列計算の顕著な劣化がみられた。これは、33cpu以上ではデータ転送に高速光インターコネクト(4GB/sec)を用いずに、GbEを使用しているため(-ldt 0)であり、センターシステムのハード的制限による。このように、これまでのPRIMEPOWER HPC2500(ngrd)のテストでは33cpu以上の高効率並列計算は実現できなかった。また、24cpu使用時のコンパイルオプションの違いによるハードバリアとソフトバリア利用の計算速度は、それぞれ21.82 Gflopsと20.27 Gflopsであり、そのハードバリアとソフトバリアの差は約7.1%であった。HPC2500は1ノード当たり最大128cpuの構成であるから、128cpuでどこまで高速計算ができるか、更に10ノード(128cpu/node)1280cpuでどうか、最大の関心事である。
今後、富士通のベクトル並列機VPP5000はスカラー並列機PRIMEPOWER HPC2500に更新されることになろう。ベクトル並列機で高効率であったプログラムがスカラー並列機でも高効率が保証されるのか、特に大規模計算では見通しが立たない。ベクトル並列機とスカラー並列機は根本的に異なる。例えば、ベクトル並列機では最内のdo loopでベクトル化して、最外のdo loopで並列化するのが基本であった。従って、計算効率を上げるためには最内のdo loopは長い方が望ましかった。しかし、スカラー並列機はキャッシュのヒットが高速計算に不可欠となる。1次キャッシュと2次キャッシュのヒット、largepageの機能で高速計算を保証している。従って、計算に関与する変数の番地はあまり離れていないことが望ましいことになる。大規模コードではこれは深刻な問題となる。3次元MHDコードの配列の順序をf(nx2,ny2,nz2,nb)からF(nb,nx2,ny2,nz2)に変更しているのは、正にその問題解決のためである。cpu数が1000個以上になってもそれだけで高速計算が実現できるのか、大変疑問である。やはり、大規模シミュレーションMHDコードで高効率並列計算を実現するためには、キャッシュの利用を考慮した、スカラー並列機用の新しい3次元MHDコードを新たに作らなければならないのだろうか?その一つの解は、プログラムを変えなくても2次元目をスレッド並列(自動並列、あるいはOpenMPを使用したノード内並列)、3次元目をプロセス並列(MPI)で並列化すれば高速計算が可能であろうと富士通SEからコメントがあったが、大変興味のある今後の課題である。また、3次元領域分割を基本にする新しい3次元MHDコードの開発はもう一つの解であろうと思われる。
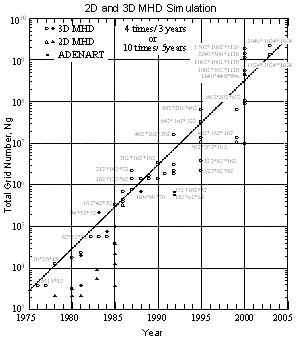 | 図10 総格子点数でみた2次元と3次元MHDシミュレーションの年毎の発展、総格子点数は3年で4倍あるいは5年で10倍に増加1回の時間ステップを進めるために必要とする |
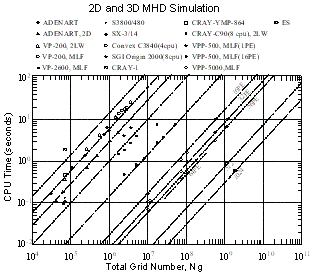 | 図11 MHDシミュレーションの総格子点数に対する 計算時間 |
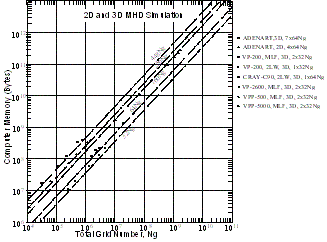 | 図12 MHDシミュレーションの総格子点数に対する必要な計算機メモリの総容量 |
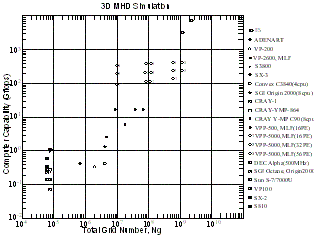 | 図13 MHDシミュレーションの総格子点数に対するコンピュータの絶対処理能力の比較 |
7.地球磁気圏の3次元グローバルMHDシミュレーションの将来
太陽風と地球磁気圏相互作用のグローバルMHDシミュレーションを約25年間行ってきたが、その推移をまとめ、実際のシミュレーション実行のデータを基にして将来を展望してみる。先ず、各年度でどのくらいの2次元と3次元の総格子点数を用いたMHDシミュレーションを実行することができたかを示したのが10図である。1982年からCRAY-1を用いた地球磁気圏の3次元グローバルMHDシミュレーションに着手し、 使用格子点数は、62*32*32、50*50*26と増大したが、CRAY-1では主メモリの大きさ (1MW)が制限であった。その後、国産のベクトル機が開発されて、Fujitsu VP-100, VP-200及びVP-2600の使用によって 100の3乗を越す3次元MHDシミュレーションを行うことができるようになった。更に1995年からベクトル並列機VPP500が、そして2000年にVPP5000が使用できるようになり、1000の3乗の格子点数を用いた3次元MHDシミュレーションも現実のものとなった。 利用できる総格子点数からみたMHDシミュレーションの年毎の発展拡大の傾向をみると、 この25年間破線で示すように、平均して3年で4倍あるいは5年で10倍の割合で増大している。
11図にMHDシミュレーションを実行する場合、時間ステップを1回だけ進めるのに必要とする計算時間を、12図にMHDシミュレーションで用いる総格子点数に対する計算機メモリの必要総容量を示す。Earth Simulator(ES)で512cpuと1024cpuを使用した場合の計算時間も示してある。計算機の種類と計算方法にも依存するが、通常総格子点数に比例して計算時間は長くなり必要計算機メモリも増大する。地球磁気圏のMHDシミュレーションでは、数千回から数万回の時間ステップを繰り返し計算するので、1回の時間ステップを進めるのに必要とするcpu timeは大体10秒以下でないと実用にならない。こうして、計算機の計算速度から使用できる3次元格子点数の大きさが決まり、同時に、その3次元格子点数を用いた時の3次元MHDプログラムサイズが計算機主メモリに収まる必要がある。
MHDモデルでは、密度、速度3成分、圧力、磁場3成分の8成分の時間発展を解くので、総格子点数をNgとした時独立な変数は8Ngで、容量は単精度で32Ng Bytesになる。MHDモデルの必要不可欠の変数量は 2 step Lax-Wendrotf法(2LW)を用いた場合32Ng Bytesが、Modified Leap-Frog法(MLF)を用いた場合、2つの時刻の変数を同時に保持するために64Ng Bytesが必要となる。多種類のベクトル機で実行していた3次元MHDコード(2LW, MLF)では、作業変数を徹底的に減らした結果、プログラムサイズは必要不可欠な変数量の1.3倍以内に収まっていたが、並列機になって作業変数を減らすことはほとんど不可能になり、プログラムサイズがかなり増大した。しかし、VPP500やVPP5000ではその増加の割合も、MLF法使用の場合で必要不可欠の変数量の約2.5倍(160Ng=2.5*64Ng) に収まっている。こうした総格子点数に対する計算速度と必要計算機メモリの関係を調べておくと、新しい研究テーマを設定する際、どれだけ大きな3次元 MHDシミュレーションを実行することができるか、そして将来の見通しはどうかをかなり正確に予測できる。
MHDシミュレーションで用いる総格子点数に対する種々の計算機による絶対処理能力の比較をまとめたものを13図に示す。ベクトル機からベクトル並列機への移行で計算機の処理能力は飛躍的に高くなり、最近の高性能のワークステーションやパーソナルコンピュータは、一昔前のスーパーコンピュータの計算速度(0.3 Gflops程度)に達している。しかし、最大級のスーパーコンピュータは常にそれらの約千倍の高速計算処理能力を有している。多数の3次元格子点を用いた大容量シミュレーションでは、メモリ不足やRISC計算機でのcache不足などによって、更に決定的な差が生じる。フルベクトル化/フル並列化されたプログラムを用いて、VPP5000等のスーパーコンピュータで100時間かかる3次元MHDシミュレーションは、スーパーコンピュータ以外の通常のワークステーションやパーソナルコンピュータで実行することは全く不可能である。地球磁気圏の3次元グローバルMHDシミュレーションなどの大型コンピュータシミュレーションを実行するためには、最大級のスーパーコンピュータの利用は常に必須の条件と言える。現在までの最大計算速度はVPP5000(64cpu)で441 Gflops、Earth Simulator(ES, 1024cpu)で7.1 Tflopsが得られている。
8.おわりに
名古屋大学情報連携基盤センターにグリッドシステムとして導入されたPRIMEPOWER HPC2500(ngrd)の性能評価を、MPIで書かれた地球磁気圏の3次元MHDシミュレーションコードを用いて行った。ベクトル並列機VPP5000から、クラスター型スカラー並列機PRIMEPOWERへの移行であったために、計算効率を上げるためにいくつかの困難に直面したが、32cpuまでの利用ではスケーラビィティもかなりよく、グリッド数(nx,ny,nz)=(500,318,318)を用いた場合、2cpuで21%(=0.116/5.2)の実行効率があり、更に8cpu で8.4 Gflops、32cpuで25.8 Gflopsの計算速度を実現するまで改良できた。33cpu以上ではセンターシステムのデータ転送におけるハード的制限のために高効率の計算は実現できなかった。ただし、今回はスレッド並列は用いずに、MPIによるプロセス並列ジョブの測定だけであった。
富士通のスーパーコンピュータもベクトル並列機VPP5000から、後継機種としてクラスター型のスカラー並列機PRIMEPOWER HPC2500に替わることになる。ベクトル並列機で高効率を実現していたプログラムがそれ相応の高効率並列計算をスカラー並列機でも実現できるのか?この問題が、多くの大規模シミュレーション研究者にとっての大きな関心事であろう。米国のほとんどの一般ユーザーのプログラムは、大規模のスカラー並列機(MPP)で高効率を実現できていないと言われている。気象の大規模シミュレーションコードでは、3-7%の実行効率と言われているし、米国DOEの全科学分野の大規模シミュレーションコードでは、10%の実行効率の実現を目標としている。また、最近の米国ASCIプロジェクトの中で、ノード内自動並列、ノード間利用者による並列化で高効率計算を実現するはずのものが、実際には高効率が実現できなので困っているとも聞いている。このように、大規模スカラー並列機での高効率並列計算はほとんど実現されたことがない、非常に困難な問題であり、新しい挑戦である。
富士通のスーパーコンピュータPRIMEPOWER HPC2500は、設計思想としてスレッド並列(自動並列、あるいはOpenMPを使用したノード内並列)とプロセス並列(MPI等を使用したノード間並列)との併用による並列ジョブの実行を想定していて、最大性能を引き出すにあたってはやはりその構成が望ましいと聞いている。そのような最適の並列化手法を駆使して、PRIMEPOWER HPC2500で更にcpu数を増やしてTflopsの実行速度が実現すること、最大規模の構成でEarth Simulatorに負けない計算速度を実現することを強く期待している。
尚、本稿で使用したMPIやHPF/JAなどで書かれた3次元MHDコードの基本形とその説明、計算速度を測定したプログラムなどは次のホームページに載せている。
コンピュータシミュレーション
http://gedas.stelab.nagoya-u.ac.jp/simulation/simulation_j.html
科学研究費基盤研究(A)(1)
「共通並列計算電磁流体・粒子コードによる太陽風磁気圏電離圏ダイナミックスの研究」
http://center.stelab.nagoya-u.ac.jp/kaken/kakenhi.html
9.謝辞
本稿の3次元MHDコードの計算速度測定は名古屋大学情報連携基盤センターのスーパーコンピュータ、Fujitsu VPP5000/64とPRIMEPOWER HPC2500 (ngrd)を利用してなされたものです。また、VPP FortranからHPF/JAとMPIへの書き換えとPRIMEPOWER HPC2500の利用で多くの助言を頂いた富士通株式会社のSEの方に、更に、MPIへの原型の書き換えではお世話して頂いた国立極地研究所の岡田雅樹助手と日立製作所のSEの方に感謝いたします。
[参考文献]
[1] T. Ogino, A three-dimensional MHD simulation of the interaction of the solar wind with the
earth's magnetosphere: The generation of field-aligned currents,
J. Geophys. Res., 91, 6791-6806 (1986).
[2] T. Ogino, R.J. Walker and M. Ashour-Abdalla, A global magnetohydrodynamic simulation of the
magnetosheath and magnetopause when the interplanetary magnetic field is northward,
IEEE Transactions on Plasma Science, Vol.20, No.6, 817-828 (1992).
[3] T. Ogino, Two-Dimensional MHD Code, (in Computer Space Plasma Physics), Ed. by H.
Matsumoto and Y. Omura, Terra Scientific Publishing Company,
161-215, 411-467 (1993).
[4] T. Ogino, R.J. Walker and M. Ashour-Abdalla, A global magnetohydrodynamic simulation of the
response of the magnetosphere to a northward turning of the interplanetary magnetic field,
J. Geophys. Res., Vol.99, No.A6, 11,027-11,042 (1994).
[5] 荻野竜樹、「太陽風と磁気圏相互作用の電磁流体力学的シミュレーション」,
プラズマ・核融合学会誌,CD-ROM 特別企画(解説論文), Vol.75, No.5, CD-ROM 20-30, 1999.
http://gedas.stelab.nagoya-u.ac.jp/simulation/mhd3d01/mhd3d.html
[6] 荻野竜樹、「太陽風磁気圏相互作用の計算機シミュレーション」,
名古屋大学大型計算機センターニュース, Vol.28, No.4, 280-291, 1997.
[7] 荻野竜樹、「コンピュータシミュレーションと可視化」,
愛媛大学総合情報処理センター広報, Vol.6, 4-15, 1999.
http://gedas.stelab.nagoya-u.ac.jp/simulation/simua/ehime985.html
[8] 荻野竜樹,「VPP FortranからHPFへ」,名古屋大学大型計算機センターニュース 解説,
372-405, Vol.31, No.4, (2000).
http://gedas.stelab.nagoya-u.ac.jp/simulation/hpfja/hpf013.html
[9] Ogino, T., Global MHD Simulation Code for the Earth's Magnetosphere Using HPF/JA,
Special Issues of Concurrency: Practice and Experience, 14, 631-646, 2002.
http://gedas.stelab.nagoya-u.ac.jp/simulation/hpfja/mhd00.html
[10] 荻野竜樹,「地球磁気圏のMHDシミュレーションと可視化」,天体とスペースプラズマのシミ
レーションセミナー(流体・磁気流体コース、アドバンストコース、プラズマ粒子シミュレ
ーションコース) 講義テキスト,107-136, (2003).
「並列3次元MHDコードと3次元可視化」
http://center.stelab.nagoya-u.ac.jp/kaken/mpi/mpi-j.html
[11] 津田知子、「新スーパーコンピュータVPP5000/56の利用について」、
名古屋大学大型計算機センターニュース、Vol.31, No.1, 18-33, 2000.
[12] 津田知子、「MPIによる並列化」、名古屋大学情報連携基盤センター MPI講習会資料、
2002年2月
[13] High Performance Fortran Forum, 「High Performance Fortran 2.0 公式マニュアル」、
Springer, 1999.
[14] 富士通株式会社、「HPFプログラミング 〜並列プログラミング(HPF編)
UXP/V 第1.0 版、2000年6月.
[15] 富士通株式会社、「VPP FORTRANプログラミング」、UXP/V, UXP/M
第1.2版、1997年4月.
[16] 富士通株式会社、「MPIプログラミング 〜Fortran, C〜」第1.3版、2001年4月.
[17] 富士通株式会社、「MPI使用手引き書 V20用」、UXP/V 初版 1999年9月
[18] 青山幸也(日本アイ・ビーエム株式会社)、「並列プログラミング虎の巻 MPI版」
虎の巻シリーズ2、2001年1月.
[19] 株式会社日立製作所、「スーパーテクニカルサーバSR8000プログラム移植報告書」
国立極地研究所、2002年3月.
[20] 名古屋大学情報連携基盤センター、「スーパーコンピュータVPP5000利用の手引き」
2002年4月.
「VPP5000利用の手引きのpdfファイル」
http://nucc.cc.nagoya-u.ac.jp/CENT/vpp_tebiki.pdf
「スーパーコンピュータ VPP5000/64 利用案内」のHomepage
http://www2.itc.nagoya-u.ac.jp/sys_riyou/vpp/vpptebiki.htm